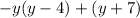
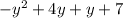
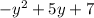
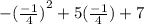
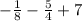
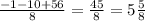
Объяснение:
Вираз {\displaystyle 0^{0}}{\displaystyle 0^{0}} (нуль в нульовому степені) багато підручників вважають невизначеним і позбавленим сенсу[1]. Пов'язано це з тим, що функція двох змінних {\displaystyle f(x,y)=x^{y}}{\displaystyle f(x,y)=x^{y}} в точці {\displaystyle (0,0)}{\displaystyle (0,0)} має неусувний розрив. Справді, уздовж додатного напрямку осі {\displaystyle X,}{\displaystyle X,} де {\displaystyle y=0,}{\displaystyle y=0,} вона дорівнює одиниці, а вздовж додатного напрямку осі {\displaystyle Y,}{\displaystyle Y,} де {\displaystyle x=0,}{\displaystyle x=0,} вона дорівнює нулю. Тому ніяка домовленість про значення {\displaystyle 0^{0}}{\displaystyle 0^{0}} не може дати неперервну в нулі функцію.
Деякі автори пропонують домовитись про те, що цей вираз дорівнює 1.
1)из первых двух уравнений:
z=7-2x-y
z=8-x-2y приравниваем 7-2x-y=8-x-2y , выразим y (можно было бы и выразить х, как кому удобнее) приводим подобные и получаем у=1+х
2) из 3 ур-я выражаем z : 2z= 9-x-y, z=(9-x-y)/2 в это уравнение вместо у подставляем значение которое у нас получилось в 1 пункте: z= 4-x
3) из первого ур-я выражаем z : z=7-2x-y сюда вместо у подставляем значение которое получили в пункте 1, получается z=7-2x-1-x=6-3x
4)приравниваем пункт 2 и 3, получается 6-3x=4-x, х=1
5) мы нашли что у=1+х=1+1=2
6) мы нашли что z=4-x=4-1=3
проверка
в ур-е 1 подставим полученные значения
2*1+2+3=7
7=7