f(x) = 5 +2x - 3
f(x) = 2x + 2
Есть несколько начертить этот график, но в конечном итоге получается одно и то же. Мне больше нравится этот:
1) Строим график функции f(x) = x. Это будет прямая, построенная под углом 45° к оси Ох (пунктирная линия на графике)
2) Теперь строим график функции f(x) = 2x путём сжатия исходного графика к оси Оу. Выглядит это так (прямая, выходящая из начала координат, которая не пунктирная).
3) Ну и наконец, смещаем полученный график на 2 единицы вверх (прямая, выходящая из точки 2 на оси Оу, самая тёмная на рисунке)
Когда разберётесь с этим, можно опускать эти пункты и сразу строить конечный, но на первых порах лучше максимально разобрать этот процесс
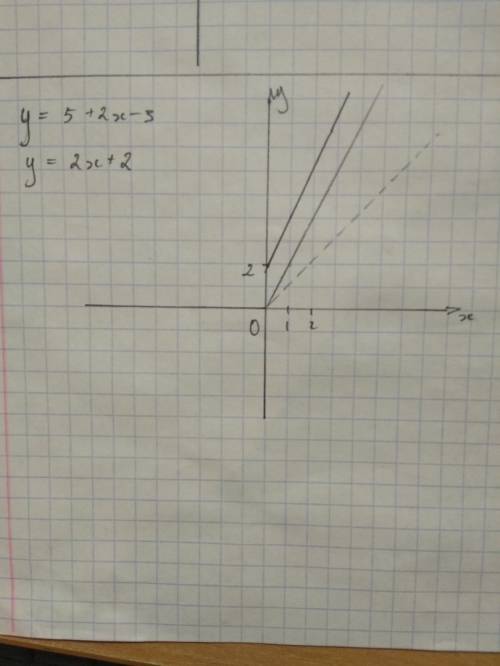
{ a₂ +a₄ = 16 ; a ₁ * a₅ = 28 .⇔{ (a₁+d) + (a₁+3d)= 16 ;a₁* (a₁+4d) =28.⇔
{a₁+2d=8 ;a₁(a₁+4d)=28 . ⇔ {a₁ = 8 -2d ; ( 8 -2d )(8+2d) =28 .
⇔{ a₁ = 8 -2d ; ( 4 -d )(4+d) =7. ⇔{a₁ = 8 -2d ; 16 -d ² =7 .
⇔{ a₁ = 8 -2d ; d = ± 3 . ⇔ [ { d = - 3 ; a =14 ; { d = 3 ; a = 2
ответ : 14 ; 11; 8 ; ... или 2 ; 5 ; 8 ;...
* * * * * * * * * * * * * * * * * *
a(n) → a₁ ; a₂ ; a₃ ;
a₁(n) → a₁² ;a₂² ; a₃² ; ...
a(n) → a₁ ; a₁q ; a₁q² ; ; где |q| <1 .
a₁(n)→ a₁² ; (a₂)² ; (a₃)² ; ... ⇔ a₁² ; a₁²*(q² ) ; a₁²*(q²)² ; ...где q²=q₁< 1
S₁ = a₁²+ a₁²*(q² ) + a₁²*(q²)² + ... = a₁² / (1-q₁²).