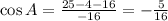; Тогда синус этого угла равен 
;
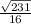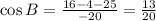; Синус этого угла: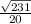
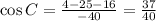; Синус этого угла:
;
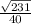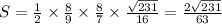
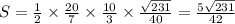
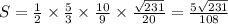
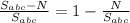- полученный результат и есть искомое соотношение. Найдем 
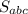: по формуле Герона получаем 
; 
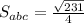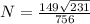; Итак, искомое отношение равно: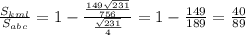 
1.
1)Функция у=sin х периодическая - ВЕРНО
2)Множество значений функции у=3/х-все действ. Числа - НЕВЕРНО
3)log4(.0.16) не существует НЕВЕРНО
4)15^-8 положительное число ВЕРНО
2.
1)Функция у=tg х периодическаЯ ВЕРНО
2)Множество значений функции у=3х-все действ. Числа ВЕРНО
3)log4(-0,16) не существует ВЕРНО
4)(1,5)^-8 отрицательное число НЕВЕРНО
3.
1)1)Функция у=lg х периодическаЯ НЕВЕРНО
2)Множество значений функции у=3x/x^2 все действ. Числа НЕВЕРНО
3)log4(0,16) существует ВЕРНО
4)1,5^-8 неотрицательное число ВЕРНО
4.
1)Функция у=sin x+1х периодическаЯ НЕВЕРНО
2)Множество значений функции у=3х/x все действ. Числа НЕВЕРНО
3)log-4(0,16) существует НЕВЕРНО
4)(-5)^-8 положительное число ВЕРНО
5.
1)Функция у=3+sin х периодическаЯ ВЕРНО
2)Множество значений функции у=х-все действ. Числа ВЕРНО
3)log4(0)существует НЕВЕРНО
4)(-5)^-4 положительное число ВЕРНО
12+10=5х-4х
22=х проверка 4(22+3)=5(22-2)=100
2)-2х+10+3х-12=4х+1
х-2=4х+1
х-4х=1+2
-3х=3 х= -1 Проверка -2 *(-1-5) +3*(-1-4)=4*(-1)+1= 12-15=-3
3) 3х-3=2х+4
3х-2х=4+3
х=7 Проверка 3(7-1) = 2(7+2) =18
4)3х-15-2х-8=-5х+1
х-23=-5х+1
х+5х=1+23
6х=24 х=4 Проверка 3(4-5)-2(4+4)=-5*4+1= -19