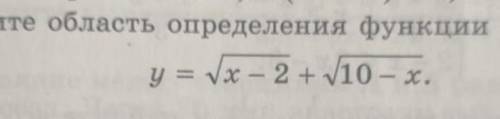
Подкоренное выражение корня чётной степени должно быть неотрицательным, то есть ≥ 0 .
![y=\sqrt{x-2}+\sqrt{10-x}\\\\\left \{ {{x-2\geq0 } \atop {10-x\geq0 }} \right.\\\\\left \{ {{x\geq } 2\atop {-x\geq-10 }} \right.\\\\\left \{ {{x\geq2 } \atop {x\leq10 }} \right. \ \Rightarrow \ \boxed{x\in[2 ; \ 10] }](/tpl/images/4420/7258/57bf5.png)
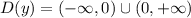
 получается с растягивания графика
получается с растягивания графика 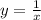 (обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности.
(обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности. тоже является гиперболой.
тоже является гиперболой.
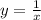 принимает отрицательные значения на луче
принимает отрицательные значения на луче 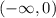 то и
то и  принимает отрицательные значения на луче
принимает отрицательные значения на луче 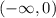
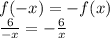

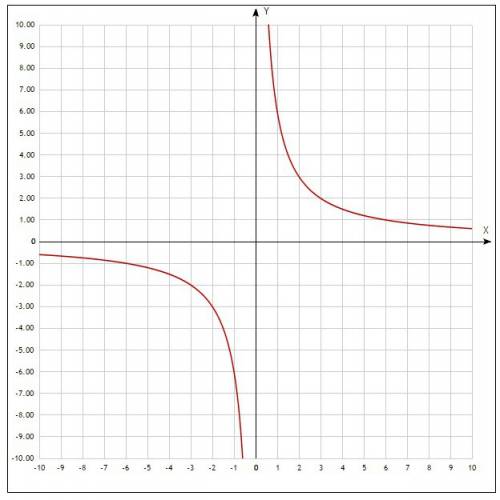
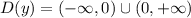
 получается с растягивания графика
получается с растягивания графика 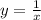 (обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности.
(обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности. тоже является гиперболой.
тоже является гиперболой.
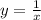 принимает отрицательные значения на луче
принимает отрицательные значения на луче 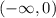 то и
то и  принимает отрицательные значения на луче
принимает отрицательные значения на луче 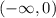
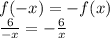


Найти область определения
Найдем область определения, отыскав промежутки, на которых уравнение определено.
Запись в виде интервала:
[2,10]
Нотация построения множества:
{x|2≤x≤10}