
Есть и другие упростить данную дробь, однако я предпочитаю этот , так как, на мой взгляд, он довольно простой и самое главное - быстрый.
Наша задача представить слагаемое "2х" в виде суммы/разности двух слагаемых так, чтобы из всех получившихся слагаемых в числителе можно было что-то вынести за скобку.
Таким образом, представим "2х" как разность "3х-x" (так как "3х-х=2х"):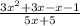
Сразу видно, что можно вынести общий множитель "3x" в числителе у двух слагаемых. Также вынесем общий множитель "5" из выражения в знаменателе.
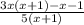
Необходимо в числителе создать ещё одну скобку, которую мы также вынесем в качестве общего множителя. Заметно, что можно вынести "-1" или просто минус "-" из числителя в части "-х-1", чтобы после вынесения получилось "x+1", которую мы вынесем, как общий множитель.
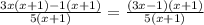
Сократим общий множитель "x+1", после чего выражение будет упрощено.

ответ: 
2^(x-1) -2^(x-6) > 17 ;
(2^(x-6) ) *(2^5 -1) >17 ;
2^(x-6) > 17/31 ;
x-6 > Log_2 17/31 ;
x > 6 + Log_2 17/31 иначе x∈( 6 + Log_2 17/31 ;∞) .
---
было бы лучше :
2^(x-1) +2^(x-5) > 17 ;
(2^(x-5))*(2⁴+1) >17
2^(x-5) > 1 ;
2^(x-5) > 2⁰ ;
x-5 > 0 ⇒ x >5 иначе x∈(5 ;∞).
2.
5^(3x) +3*5^(3x-2) < 140 ;
5^(3x-2) * (5² +3) < 140 ;
5^(3x-2) < 5 ;
3x-2 <1 ⇒ x <1 иначе x∈(-∞ ; 1).
ответ : x∈( - ∞ ;1).
3.
3^(x+2)+3^(x-1) ≤28 ;
3^(x-1)* (3³+1) ≤ 28 ;
3^(x-1)*28 ≤ 28 ;
3^(x-1) ≤ 1 ;
3^(x-1) ≤ 3⁰ ;
x-1 ≤ 0 ;
x ≤ 1 иначе x∈ (-∞ ; 1].
ответ : x∈( - ∞ ;1].