(Аппарат элементарных преобразований графиков функций)
График функции можно получить из графика функции , то есть:
1. График смещаем на 1 вправо.
2. Отражаем его зеркально по оси значений (a.k.a. ординат).
3. Растягиваем его по оси значений в два раза.
Получаем фигуру 1.
Найдите точки пересечения графика этой функции с осями координат.
y=-2x+2
Сначала x=0, потом y=0.
От x=0 имеем y=2.
От y=0 имеем -2x+2=0 => x=1. Точка x=1,y=0.
Найдите значение функции, если значение аргумента равно -1.
При каком значении х функция принимает значение, равное 8?
-2x+2 = 8
-2x=6
x=-3
Принадлежит ли графику функции точка А(10;-18)?
Щас проверим. . Да. Принадлежит.
Найдите точку пересечения графика данной функции и функции y=4.
-2x+2 = 4
-x+1=2
-x=1
x=-1
Точка x=-1,y=4.
(Аппарат элементарных преобразований графиков функций)
График функции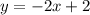
можно получить из графика функции 
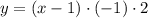, то есть:
1. График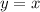
смещаем на 1 вправо.
2. Отражаем его зеркально по оси значений (a.k.a. ординат).
3. Растягиваем его по оси значений в два раза.
Получаем фигуру 1.
Найдите точки пересечения графика этой функции с осями координат.
y=-2x+2
Сначала x=0, потом y=0.
От x=0 имеем y=2.
От y=0 имеем -2x+2=0 => x=1. Точка x=1,y=0.
Найдите значение функции, если значение аргумента равно -1.
При каком значении х функция принимает значение, равное 8?
-2x+2 = 8
-2x=6
x=-3
Принадлежит ли графику функции точка А(10;-18)?
Щас проверим.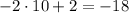
. Да. Принадлежит.
Найдите точку пересечения графика данной функции и функции y=4.
-2x+2 = 4
-x+1=2
-x=1
x=-1
Точка x=-1,y=4.