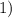
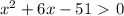
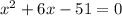
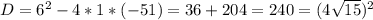
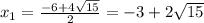
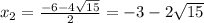
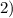
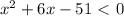
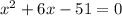
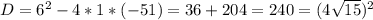
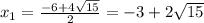
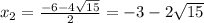
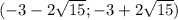
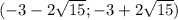
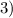
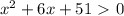
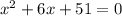
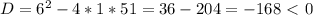
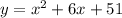
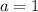∈ 
∞ 
∪ 
∞ 
∞ ∪ ∞ 
∈ 
положительный, то ветви параболы направлены вверх, а поскольку 
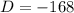отрицательный, то парабола не пересекается с осью 
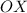. Поэтому парабола 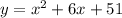расположена над осью 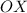; таким образом, при любом значении x имеем y>0. Значит, 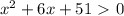при любом значении x. ∞ 
∞ 
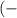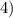
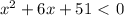
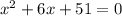
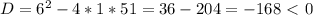
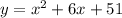
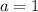положительный, то ветви параболы направлены вверх, а поскольку 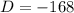отрицательный, то парабола не пересекается с осью 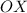. Поэтому парабола 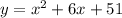расположена над осью 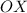; таким образом, при любом значении x имеем y>0. Значит, 
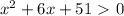при любом значении x. Следовательно, рассматриваемое неравенство не имеет решений. 
в) Преобразуем числитель. (1-cos²x+sin²x)/(x*tg3x)=2sin²x/(x*tg3x), подведем данную запись под первый замечательный предел. При икс, стремящемся к нулю, sinx ; tg3x эквивалентны х и 3х соответственно, а потому получим предел дроби 2*х*х/(х*3х) и он равен 2/3.
ответ 2/3
г) преобразуем (4-x)*(㏑(2-3х)-㏑(5-3х))=(4-x)*(㏑((2-3х)/(5-3х))=
(4-x)㏑((3х-2)/(3х-5))=(4-x)㏑((1+3/(3x-5))=㏑((1+3/(3x-5))^(4-x)
cвели решение ко второму замечательному пределу, возьмем сначала предел от (1+3/(3x-5))^(4-x), а затем логарифм от полученного предела.
представим (1+3/(3x-5))⁽⁴ ⁻ˣ⁾=(((1+(3/(3x-5)))⁽³ˣ ⁻⁵⁾/³))⁽³⁽⁽⁴⁻ˣ⁾/⁽³ ˣ⁻⁵)предел от этого выражения равен е⁻¹, а ㏑е⁻¹=-1*lnе=-1
ответ -1
