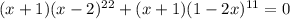
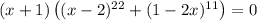
Уравнение распадается на два. Рассмотрим первое уравнение:
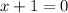
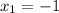
Рассмотрим второе уравнение:
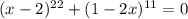
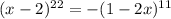
Заметим, что в левой и правой части стоят 11 степени некоторых выражений. Так как функция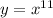 
монотонно возрастает на всей области определения, то для этой функции можно сделать вывод: значения функций равны когда равны значения аргументов. Запишем:
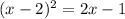
Дорешаем это уравнение:
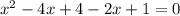
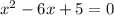
В соответствии с теоремой Виета:
Нетрудно заметить, что этим условиям удовлетворяют числа 1 и 5, но нас больше интересует именно их произведение:
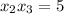
Тогда, произведение всех корней:
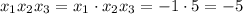
ответ: -5
1) (3;3) 2) (1;-1)
Объяснение:
при таких координатах дані завдання виконуються