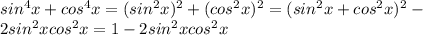
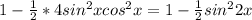
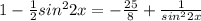
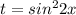и продолжать решение уже дробно-рационального уравнения.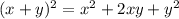
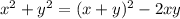
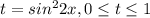
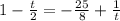
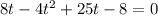
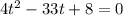
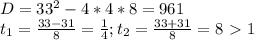- этот корень не удовлетворяет нашему уравнению.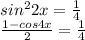
1) (18a-3a²)/(8a²-48a)=3a(6-a)/8a(a-6)=3a(-1)(a-6)/8a(a-6)=-3/8
2) (8p-40)/(15-3p)=8(p-5)/3(5-p)=8(-1)(5-p)/3(5-p)=-8/3
3) (4-x²)/(10-5x)=(2-x)(2+x)/5(2-x)=(2+x)/5=2/5+x/5=0.4+0.2x
4) (3x+6y)²/(5x+10y)=9(x+2y)²/5(x+2y)=9(x+2y)/5=1.8(x+2y)=1.8x+3.6y
5) (ax+bx-ay-by)/(bx-by)=(x(a+b)-y(a+b))/b(x-y)=(a+b)(x-y)/b(x-y)=(a+b)/b=a/b+1
6) (a²-6a+9)/(27-a³)=(a-3)²/(3-a)(9+3a+a²)=(a-3)²/(-1)(a-3)(9+3a+a²)= =(3-a)/(9+3a+a²)
7) (2a-2b)²/(a-b)=4(a-b)²/(a-b)=4(a-b)=4a-4b
8) (4c+12d)²/(c+3d)=16(c+3d)²/(c+3d)=16(c+3d)=16c+48d
9) (4x²-y²)/(6x-3y)²=(2x-3y)(2x+3y)/9(2x-y)²=(2x+y)/9(2x-y)
10) (ab-3b-2a+6)/(15-5a)=(b(a-3)-2(a-3))/5(3-a)=(a-3)(b-2)/5(3-a)= =(a-3)(b-2)/5(-1)(a-3)=(2-b)/5
Объяснение:
x²-14x+49+3=x²-2²
x²-14x+49+3-x²+4=0
56-14x=0
x=56/14
x=4