
нехай шв. 1-го велосипедиста - х; 2-го - у
Відстань, яку проїхав 1-й велосипедист о зустрічі, нехай буде А, тоді другий проїхав 80-А.
1-му залишилося проїхати 80-А з швидкістю х
х=(80-А)/80
2-му задишилося проїхати А з швидкістю у
у=А/180
до зустрічі вони їхали однаковий час
А/х=(80-А)/у
Підставимо в це рівняння х і у з двох попередніх
80А/(80-А)=180(80-А)/А
Скоротимо на 20
4А/(80-А)=9(80-А)/А
Зведемо до спільного знаменника
4А^2/A(80-A)=9(80-A)^2/A(80-A)
4А^2=9(80-A)^2
4А^2=9(6400-160A+A^2)=57600-1440A+9A^2
5A^2-1440A+57600=0
A(1)=(1440-sqrt(2073600-1152000))/10=(1440-sqrt(921600))/10=144-96=48
Другий корінь не підходить, бо значення не може бути більшим 80.
Отже x=(80-48)/80=32/80=0,4 (км/хв)= 24 (км/год) -шв. 1-го велосипедиста
y=48/180=16/60=16/1=16 (км/год) -шв. 2-го велосипедиста
Решите уравнение
(X+1)^2/3-(X-1)/2=(8X-1)/6
(X+1)^2/3-(X-1)/2=(8X-1)/6 |*6
2(X+1)^2-3(X-1)=8X-1
2x^2+4x+2-3x+3-8x+1=0
2x^2-7x+6=0
D=49-4*2*6=1
x=1,5
x=2
Решите уравнение
(2X-3)^2-2(5X-4)(X+1)=-9-13X
(2X-3)^2-2(5X-4)(X+1)=-9-13X
4x^2-12x+9-2(5x^2+5x-4x-4)+9+13x=0
4x^2-12x+9-10x^2-10x+8x+8+9+13x=0
6x^2+x-26=0
D=1-4*6*(-26)=625
x=-13/6
x=2
Не вычисляя корней квадратного уравнения, решите уравнение
1) 3X^2-2X-6=0
y(первое)=3X^2-2X-6
y(второе)=0
найдем координаты вершины параболы:
x(в)=-b/2a=2/6=1/3
y(в)=3(1/3)^2-2(1/3)-6=-19/3
координаты:(-19/3)
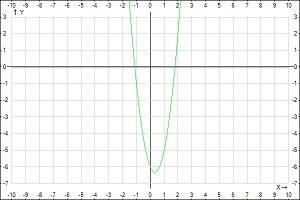
ответ:--++
Объяснение: соотношение катетов- этот tg, у подобных фигур все стороны и углы подобны