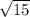В решении.
Объяснение:
График состоит из трёх частей.
1) у = х² при х <= -2;
График - часть параболы, х может быть равен или меньше -2.
Таблица:
х -2 -3 -4 -5
у 4 9 16 25 и т.д.
2) у = -2х при -2 < x < 2.
Уравнение линейной функции, график - прямая на промежутке от х= -2
до х = 2, причём х не может быть равен ни -2, ни 2, поэтому разрывы на графике.
Таблица:
х -1,9 -1 0 1 1,9
у 3,8 2 0 -2 3,8
3) у = -х² при х >= 2.
График - часть параболы, х может быть равен или больше 2.
Таблица:
х 2 3 4 5
у -4 -9 -16 -25 и т.д.
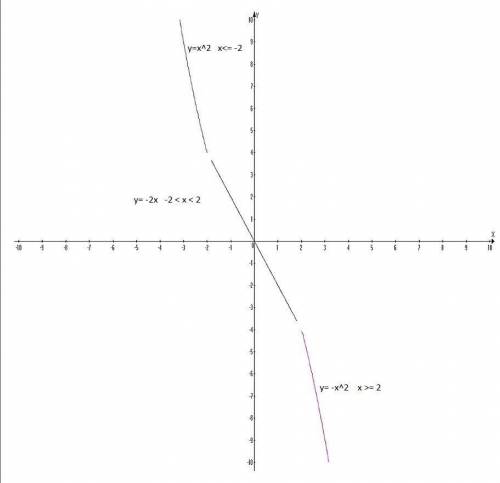
Подобные одночлены - это одночлены, которые состоят из одних и тех же букв, в одинаковых степенях, но с разными или одинаковыми коэффициентами (числовыми множителями).
В этих выражениях требуется представить одинаковые множители как степень одного множителя.
1. -3,1*babab = -3,1*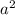
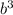 , подобным ему будет 2/5
, подобным ему будет 2/5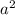
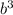
2. 2 1/3*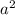 ba
ba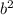 *(-3) = -7
*(-3) = -7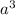
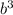 , подобным ему будет -3,1
, подобным ему будет -3,1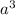
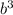
3. 1/5bab*2 = 2/5a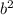 , подобным ему будет -7a
, подобным ему будет -7a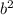
Похоже это задание на внимательность, чтобы правильно понимать смысл подобных одночленов и не вестись на одинаковые коэффициенты.
1.
1) (с-1) * (с -17) 2) -(х -3) * (х -2)
2.
1) 3 2) х+8
-------- ---------
х+ 7 -х+1
3.
1) х= -1/3; х=1/3 ; х=-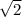 ; х=
; х=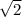
2)х=-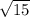 ; х=-
; х=-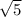 ; х=
; х=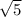 ; х=
; х=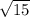
Объяснение:
3.
1)9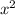 -19х+2=0
-19х+2=0
х=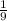
х=2
х= -1/3
х=1/3
х=-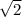
х=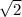
2)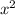 -6х-16=0
-6х-16=0
х=-2
х=8
х=-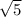
х=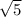
х=-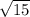
х=