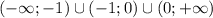5
Объяснение:
Пусть на дом задано n задач, тогда всего комбинаций решенных задач 2
n
(каждую из
задач ученик может решить или не решить). Вычтем из этих комбинаций комбинации,
когда решено менее 3 задач: 1 комбинация, когда ничего не решено; n комбинаций,
когда решена 1 задача; n(n−1)
2
, когда решено две задачи (первую решенную можно
выбрать , вторую (n − 1), при этом нам не важен порядок, поэтому делим
на 2. Итого получаем, что уникальных комбинаций, за которые учитель не поставит
оценку «2»: 2
n−1−n−
n(n−1)
2
. Для того, чтобы кто-нибудь обязательно получил оценку
«2», это число должно быть меньше, чем число учеников в классе (чтобы у каких-то
двух комбинация задач совпадала). Получаем неравенство: 2
n − 1 − n −
n(n−1)
2 < 30
наибольшее n, удовлетворяющее этому неравенству это n = 5.
ответ: 5 задач
Свойства функций
Нули функции
Нулём функции называется то значение х, при котором функция обращается в 0, то есть f(x)=0.
Нули – это точки пересечения графика функции с осью Ох.
Четность функции
Функция называется чётной, если для любого х из области определения выполняется равенство f(-x) = f(x)
Четная функция симметрична относительно оси Оу
Нечетность функции
Функция называется нечётной, если для любого х из области определения выполняется равенство f(-x) = -f(x).
Нечетная функция симметрична относительно начала координат .
Функция которая не является ни чётной ,ни нечётной называется функцией общего вида.
Возрастание функции
Функция f(x) называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е. x2>x1 → f(x2)>f(x1)
a)y=1/6x +1/(6+x)
Для начала приведем к общему знаемнателю. Общий знаменатель 6х(6+х)
Теперь будем находить ОДЗ(область допустим значений, тоже самое, что и область определения). Известно, что знаменатель дроби не может быть равен 0, поэтому
6x=0 6+x=0
x=0 x=-6
Значит х не может быть равен 0 и -6. Поэтому ОДЗ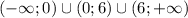
б) y=√x -√(x-4)
Мы знаем, что подкоренное выражение всегда неотрицательно, поэтому ОДЗ этой функции будет являться система неравенств
Решением системы будет являться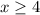
в)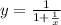
Знаменатель не может быть равен 0, поэтому
Значит х не равняется 0 и -1, а ОДЗ