
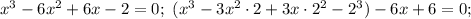
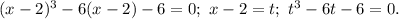
Докажем сначала, что корень единственный. Для этого исследуем функцию 
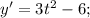 корни производной
корни производной 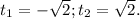
В точке  функция имеет локальный максимум, в точке
функция имеет локальный максимум, в точке 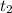 - локальный минимум, после него функция монотонно растет.
- локальный минимум, после него функция монотонно растет.
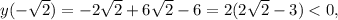 так как корень из двух меньше, чем 1,5. Итак, слева от
так как корень из двух меньше, чем 1,5. Итак, слева от  функция возрастает, справа убывает, начиная с
функция возрастает, справа убывает, начиная с 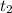 снова возрастает. Поскольку функция в точке
снова возрастает. Поскольку функция в точке  отрицательна, существует только один корень функции (и расположен он правее
отрицательна, существует только один корень функции (и расположен он правее 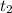 ; для нас, правда, важна только его единственность).
; для нас, правда, важна только его единственность).
Возвращаемся к уравнению  Для его решения применим метод Кардано. Замена
Для его решения применим метод Кардано. Замена 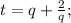 после элементарных упрощений получаем уравнение
после элементарных упрощений получаем уравнение 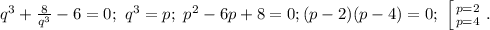
Вроде бы надо исследовать оба значения p, однако оба они дадут одно и то же значение t (кстати, ранее мы даже доказали, что двух решений быть не может). Итак, пусть p=2; ![q=\sqrt[3]{2};\ t=\sqrt[3]{2}+\frac{2}{\sqrt[3]{2}}=\sqrt[3]{2}+\sqrt[3]{4}; x=2+\sqrt[3]{2}+\sqrt[3]{4}](/tpl/images/0199/1839/61451.png)
ответ: ![2+\sqrt[3]{2}+\sqrt[3]{4}](/tpl/images/0199/1839/f6929.png)
Замечаем, что перестановки происходят отдельно среди четных чисел и среди нечетных чисел. Поэтому надо ответить на следующий вопрос: есть k предметов, расставленных в каком-то порядке слева-направо и соответствующим образом занумерованных; меняя местами за одну операцию два соседних предмета, нужно расставить их в том же порядке, но справа-налево. Говоря ученым языком, можно сказать, что сначала у нас не было ни одной инверсии (инверсия - это когда предмет с меньшим номером стоит правее предмета с большим номером), а надо сделать максимальное количество инверсий. Меняя местами соседей, мы каждый раз изменяем количество инверсий на 1. Конечно, нам невыгодно уменьшать количество инверсий, а выгодно - увеличивать. Но в каком порядке производить эту операцию - менять местами соседей - абсолютно непринципиально. Поступим, скажем, так. Поменяем сначала местами первый предмет и второй, затем первый и третий, первый и четвертый, и так далее, наконец, первый и последний. Всё. Первый предмет оказался на нужном месте и больше оттуда никуда сдвигаться не будет. Потребовалось нам для этого, естественно, (k-1) операция. Далее будем передвигать второй предмет до тех пор, пока он не поменяется местами с k-м предметом и не окажется рядом с первым, но левее первого. На это потребуется (k-2) операции. И так далее. Всего мы насчитаем  операций.
операций.
Остается подвести итоги. Окончательный ответ зависит от того, каково n - четное оно или нечетное.
1-й случай: n - четное, n=2m. Это означает, что у нас m четных чисел и m нечетных чисел. Всего операций получится
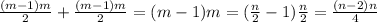
2-й случай. n - нечетное, n=2m+1. Это означает, что у нас m четных чисел и (m+1) нечетных чисел.Всего операций получится
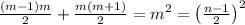
Решим задачу для n=5, 6, 7, 23.
n=5 - нечетное; 
n=6 - четное; 
n=7 - нечетное; 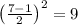
n=23 - нечетное; 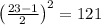
ЭТО В КАКОМ КЛАССЕ ТО А? Я ЕСЛИ ЧТО В 5А ЭТО В КАКОМ БЛИН