|x-1| + |x-a| = 1 - a
Сразу заметим, что левая часть ≥ 0, значит и правая часть должна будет тоже быть ≥ 0 :
1 - a ≥ 0
a ≤ 1
Теперь может найти подмодульные нули :
1) x - 1 = 0 2) x - a = 0
x = 1 x = a
Выставим их на числовой прямой и заметим, что а будет находиться сзади 1, так как мы выяснили что а ≤ 1, а при а = 1 есть только один корень :
x < a a ≤ x < 1 x ≥ 1
(a)(1)
Рассмотри три случая :
1) x < a
-x + 1 - x + a = 1 - a
-2x + 2a = 0
2(a - x) = 0
x = a - не подходит, т.к x < a
ответ : x ∈ ∅
2) a ≤ x < 1
-x + 1 + x - a = 1 - a
0 = 0
x ∈ R
ответ : x ∈ [a ; 1)
3) x ≥ 1
x - 1 + x - a = 1 - a
2x = 2
x = 1
ответ : x = 1
Соединим все наши решения :
[ x ∈ ∅
[ x ∈ [a ; 1)
[ x = 1
x ∈ [a ; 1]
Уравнение будет иметь ровно 3 целых решения, если а = -1.
Уравнение будет иметь 3 и больше решений при а ≤ -1
Дано:
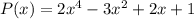
Найти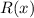 
- остаток от деления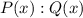 
Решение.
1) Для начала разложим многочлен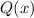 
на множители, для этого решим уравнение:
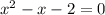
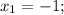
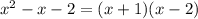
2) Так как данный многочлен 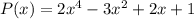делится на 
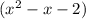с остатком, то представим его в виде
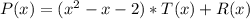
где
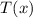- неполное частное;
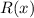- искомый остаток.
Степень остатка деления многочлена на многочлен должна быть меньше степени делителя. В данном случае делитель - многочлен второй степени, так что остаток - многочлен первой степени, который имеет вид:
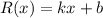
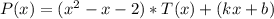
3) Подставим в равенство 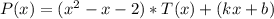первый корень 
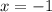и получим:
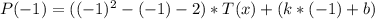
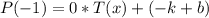
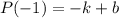
Вычислим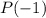 
.
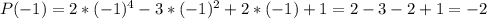
Так как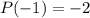 
, то
=> 
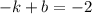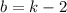
4) Аналогично решаем и со вторым корнем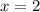 
.
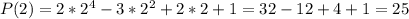
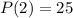
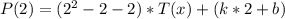
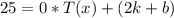
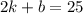
5) Подставим 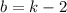в полученное уравнение:
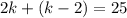
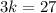
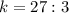
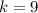
6) 
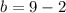
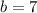
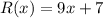- искомый остаток.
ответ: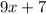 
В ( 4 ; 1 )
Объяснение: