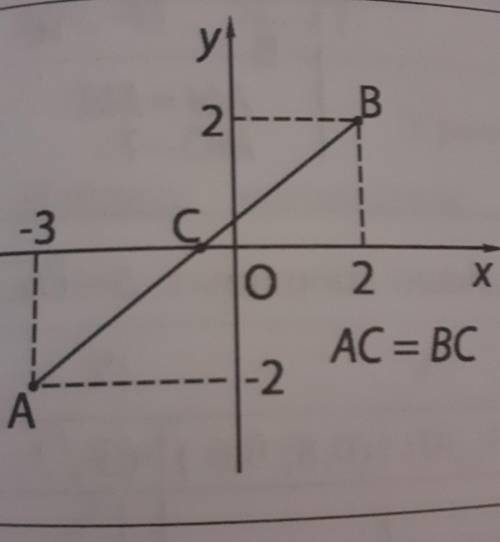
![[ -\frac{\pi}{2} ; \frac{\pi}{2} ]](/tpl/images/0597/4634/fea20.png) возрастает, а на промежутке
возрастает, а на промежутке ![[ \frac{\pi}{2} ; \frac{3\pi}{2} ]](/tpl/images/0597/4634/d8073.png) - убывает
- убывает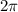 , то:
, то:![[ -\frac{\pi}{2}+2\pi n ; \frac{\pi}{2}+2\pi n ],n\in Z](/tpl/images/0597/4634/22506.png) - промежутки возрастания синусоиды
- промежутки возрастания синусоиды![[ \frac{\pi}{2}+2\pi n ; \frac{3\pi}{2}+2\pi n ],n\in Z](/tpl/images/0597/4634/745d6.png) - промежутки убывания синусоиды
- промежутки убывания синусоиды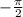 и точка
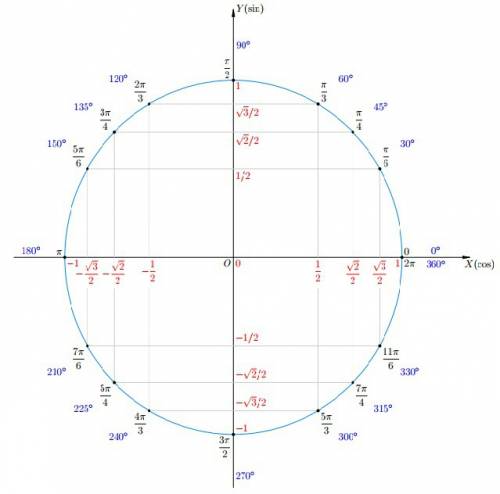
и точка 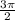 - одна и та же точка на тригонометрическом круге
- одна и та же точка на тригонометрическом круге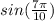 и
и 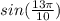
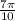
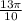
![[ \frac{\pi}{2} ; \frac{3\pi}{2} ]](/tpl/images/0597/4634/d8073.png) убывания. Так как это промежуток убывания, то если выполняется
убывания. Так как это промежуток убывания, то если выполняется 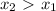 , то будет выполнятся
, то будет выполнятся 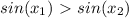
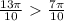
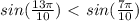
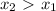 , то выполняется
, то выполняется 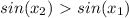
![[ \frac{3\pi}{2} ; \frac{5\pi}{2}]](/tpl/images/0597/4634/0c4f5.png)
![[- \frac{3\pi}{2} ; -\frac{\pi}{2} ]](/tpl/images/0597/4634/7af0d.png)
![[ \frac{3\pi}{2} ; \frac{5\pi}{2} ]](/tpl/images/0597/4634/5d6a9.png)
b > a или что b-a=c>0.
b = c+a
b^2=c^2+2ac+a^2
a^2-b^2 = -c^2-ac.
Левая часть по условию >0, значит и правая тоже.
Запишем -c^2-ac >0
При положительных а и с имеем положительные c^2 >0 и ac>0.
Приплюсуем их и слева и справа к обеим частям неравенства.
-c^2-ac + c^2 +ac > c^2+ас.
Получим 0> c^2+ас, что неверно. Значит исходное b>a неверно.
Поскольку а не равно b (иначе разность квадратов нулевая) ,
остаётся что верно только a>b.
Другой
Дано a>0, b>0, a^2-b^2>0.
Пусть a^2-b^2 = N >0
Тогда легко вычислить с=N/(2a+2b), причем ясно, что c>0,
так как все числа положительны.
Запишем тогда N=c(2a+2b) и тогда
a^2-b^2 = c(2a+2b) > 0
a^2 - 2ac =b^2 +2bc Дополним левую часть до квадрата.
a^2 - 2ac +с^2 =b^2 +2bc +c^2
(a-c)^2=(b+c)^2
Следовательно
(a-c)=(b+c)
a-b = 2c >0
a-b >0 или
a>b, что и тр. док-ть.