![Есурсы [3]1. Сократить дробь:8а (а-в)б)15ас24 в (в-а)5 610а с; в)в) 25 2y+y2у](/tpl/images/4437/6842/07d8a.jpg)
У выражение: (√6+√3)×√12-2√6×√3
1. Раскроем скобки:
(√6+√3)×√12=√12×√6+√12×√3=√72+√36=√72+6
2. Представим 72 как произведение 36 и 2:
√72+6=√36×2+6=√36×√2+6=6√2+6
3. Разберём подробнее 2√6×√3:
2√6×√3=2×√6×3=2×√18
4. Представим √18 как произведение чисел 9 и 2:
2×√18=2×√9×2=2×√9×√2=2×3√2=6√2
5. Подставим полученные значения (действия 2 и 4):
(√6+√3)×√12-2√6×√3=6√2+6 - 6√2=6
ОТВЕТ: 6
В одно действие:
(√6+√3)×√12 - 2√6×√3=√12×√6+√12×√3 - 2√18=√72+√36 - 2√9×2=√72+6
- 2×3√2= √36×2+6 - 6√2=6√2+6-6√2=6
Объяснение:
1) Знак неравенства меняется если основное число меньше 1;
2) Если знак неравенства, то точка будет неполная;
3) Если знак неравенства больше равно, меньше равно, то точка будет полная.
4) Полная точка ( зарисованная внутри );
5) Неполная точка ( не зарисованная внутри );
6) Если знак неравенства, то скобка "(" ;
7) Если знак неравенства больше равно, меньше равно, то скобка
"[" ;
8) В какую сторону показывает носик неравенства, в ту сторону рисуем допустимые значения;
9) Не забываем что числа можно подавать как меньшее число в степени;
Теперь когда всё вспомнили можно решать:
1)
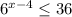
Подаём число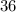
как 
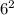
Не забываем что можно сократить основы если они одинаковые.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Фото прямых прикрепил.
Точка полная так как имеем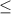
.
Допустимые значения направленные в левую сторону так как "носик" знака неравенства направлен именно туда.
x ∈ ( -∞, 6 ]
2)
Подаём число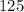
как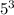 
Сменили знак неравенства, так как перенесли - в другую часть неравенства.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Точка неполная, так как имеем > .
x ∈ ( -2, +∞ )
3)
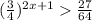
Подаём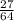
как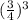 
.
Сменили знак неравенства, так как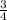
меньше 1.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Точка неполная, так как имеем
.
x ∈ ( -∞, 1 )