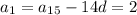Чертим прямую "Х", на ней откладываем точки -3,5 и 3. Причем обе точки заштрихованы, т.к. неравенство нестрогое. Берём любое значение x > 3 и проверяем знак нашего выражения (x-3.5)(x+3) на этом интервале. Например, возьмем х = 4: (4-3.5)(4+3) = 0,5*7=3,5>0, значит, отмечаем интервал "+". Аналогично для двух других. Изображение прикрепила. Нас устраивает промежуток с "-", т.к. знак неравенства ≤. Т.е. x ∈ [-3.5;3] или в другом формате записи: -3,5 ≤ x ≤ 3 Считаем целые решения: -3, -2, -1, 0, 1, 2, 3 - всего 7 штук
1. Используя формулу n-го члена арифметической прогрессии: an = a1 + (n-1)d, решим следующую систему уравнений
***************************************************************************************************
2.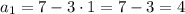
Имеем арифметическую прогрессию с первым членом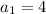 и разностью прогрессии
и разностью прогрессии 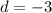
Сумма первых 12 членов арифметической прогрессии, равна:
**************************************************************************************************
3. Разность прогрессии: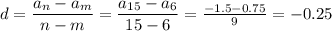
Первый член арифметической прогрессии: