
7) 6x²-x+2 ≤ 0
D = b²-4ac => (-1)²-4*6*2 = 1-48 = -47 < 0, нет корней.
ответ: нет корней.
8) x²-2x+1 ≤ 0
D = b²-4ac => (-2)²-4*1*1 = 4-4 = 0 = 0, 1 корень.
x = 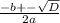
x₁ = 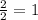
(x-1) ≤ 0
\\\\\\\\\\\\\\\\\\\\*------------------------------------->
1 x
ответ: (-∞;1).
9) 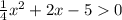
D = b²-4ac => 2²-4*0,25*(-5) = 4+5 = √9 = 3 > 0, 2 корня.
x = 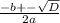
x₁ = 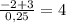
x₂ = 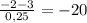
(x-4)(x+20) > 0
---------------0/////////////////////0///////////////////>
-20 4 x
ответ: (-20;4)∪(4;+∞).
Сначала нужно подобрать какое-нибудь частное решение (перебором). Это сделал кто-то (выше), итак частное решение x₀=15; y₀=-86. (подставь проверь!)
Теперь
195*x + 34*y = 1,
195*15+34*(-86) = 1,
Вычитаем из первого равенства второе равенство и получаем
195*(x-15) + 34*(y+86) = 0,
Делаем замену X = x-15; Y = y+86;
195*X + 34*Y = 0;
195*X = -34*Y;
5*3*13*X = -2*17*Y,
Так как 195 и 34 - взаимно простые, то, исходя из последнего равенства Y должно делится на 195, то есть Y = 195*A, (А - целое).
195*X = -34*(195*A),
X = -34*A,
Делаем обратные замены:
(y+86) = 195*A,
(x-15) = -34*A,
y = -86+195*A,
x = 15 - 34*A,
Подставляя эти целые решения в исходное уравнение, убеждаемся, что они верны для любого целого А.