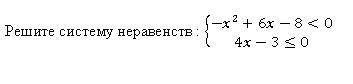
Решаем методом замены переменной.
Пусть x + y = a, xy = b
Выразим теперь сумму квадратов из второго уравнения через a и b:
(x + y)² = x² + 2xy + y² или с учётом замены
a² = x² + 2b + y²
Отсюда
x² + y² = a² - 2b
Перепишем теперь нашу систему с учётом все вышесказанного:
a = 6 a = 6 a = 6
a² - 2b = 16 + 2b -4b = 16 - a² = 16 - 36 = -20 b = 5
Теперь возвращаемся к нашим старым переменным, учитывая, что a = x + y, а b = xy:
x + y = 6 y = 6 - x
xy = 5 x(6 - x) = 5 (1)
(1) 6x - x² = 5
x² - 6x + 5 = 0
x1 = 5; x2 = 1
Получаем два варианта:
x = 5 или x = 1
y = 1 y = 5
Всё, систему мы решили
В круглых скобках стоит сумма членов арифметической прогрессии (2, 7, 12, ..., 57), где каждый следующий член получен из предыдущего прибавлением одного и того же числа d=5 (разность прогрессии).
Сумма n членов арифметической прогрессии находится по формуле
где а_{1} - первый член прогрессии, а_{n} - n-ый член прогрессии, n - число членов прогрессии.
В нашем случае, а_{1}=2, а_{n} =57.
Найдем число n членов арифметической прогрессии, используя формулу
57=2+(n-1)*5
(n-1)*5=55
n-1=11
n=12
Таким образом, искомая сумма равна