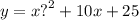
Номер 498 постройте график функции и,используя его выясните ее свойства а) $y = x {?}^{2} + 10x + 25$
и в)
мне нужно с графиком

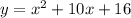
$y = {x}^{2} + 10x + 16$

👇

Увидеть ответ

Открыть все ответы

Ответ:

1lёn1

15.10.2021

y'=y-x^2

y'-y=-x^2

Первый

Решение ищем как сумму общего решения однородного уравнения, соответствующего данному неоднородному, и частного решения данного неоднородного уравнения.

Составим однородное уравнение, соответствующее данному неоднородному:

y'-y=0

Решаем уравнение с разделяющимися переменными:

y'=y

$\dfrac{dy}{dx} =y$

$\dfrac{dy}{y} =dx$

$\int\dfrac{dy}{y} =\int dx$

$\ln|y| =x+C$

Общее решение однородного уравнения:

$y=e^{x+C}$

Частное решение ищем в виде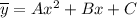 $\overline{y}=Ax^2+Bx+C$ .

Найдем производную:

$\overline{y}'=2Ax+B$

Подставим в уравнение:

2Ax+B-Ax^2-Bx-C=-x^2

-Ax^2+(2A-B)x+(B-C)=-x^2

Условие равенства левой и правой частей:

$\begin{cases} -A=-1\\ 2A-B=0 \\ B-C=0 \end{cases}$

$\begin{cases} A=1\\ 2-B=0 \\ C=B \end{cases}$

$\begin{cases} A=1\\ B=2 \\ C=2 \end{cases}$

Частное решение неоднородного уравнения:

$\overline{y}=x^2+2x+2$

Искомое решение:

$\boxed{y=e^{x+C}+x^2+2x+2}$

Второй

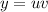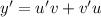Решение ищем в виде произведения двух ненулевых функций y=uv . Тогда y'=u'v+v'u .

u'v+v'u-uv=-x^2

Пусть сумма первого и третьего слагаемого в левой части равна нулю:

u'v-uv=0

u'-u=0

$\dfrac{du}{dx} -u=0$

$\dfrac{du}{dx}=u$

$\dfrac{du}{u}=dx$

$\ln|u|=x$

u=e^x

Тогда второе слагаемое в левой части равно правой части:

v'u=-x^2

$v'\cdot e^x=-x^2$

$\dfrac{dv}{dx} \cdot e^x=-x^2$

$dv=-x^2e^{-x}dx$

$\int dv=-\int x^2e^{-x}dx$

Интеграл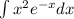 $\int x^2e^{-x}dx$ вычислим отдельно. Будем использовать интегрирование по частям: 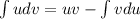$\int udv=uv-\int vdu$ (не записывая произвольную константу):

$\int x^2e^{-x}dx=\left=-x^2e^{-x}-\int(-e^{-x}\cdot2xdx)=\\=-x^2e^{-x}+2\int xe^{-x}dx=\left=\\=-x^2e^{-x}+2\left(x\cdot(-e^{-x})-\int(-e^{-x}dx)\right)=-x^2e^{-x}+2\left(-xe^{-x}+\int e^{-x}dx\right)=\\=-x^2e^{-x}+2\left(-xe^{-x}-e^{-x}\right)=-x^2e^{-x}-2xe^{-x}-2e^{-x}=-(x^2+2x+2)e^{-x}$

Таким образом:

$v=-(-(x^2+2x+2)e^{-x})+C$

$v=(x^2+2x+2)e^{-x}+C$

Искомая функция:

$y=uv=e^x\cdot\left((x^2+2x+2)e^{-x}+C\right)$

$\boxed{y=x^2+2x+2+Ce^x}$

4,7(18 оценок)

Ответ:

Sr529

15.10.2021

1) арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, получается прибавлением к предыдущему одного и того же числа.

пример: 1,2,3,410; 3,6,9,12,15

формула n-члена: аn= а1 +d(n-1)

формула для нахождения разности: d=аn+1-аn так как аn+1=аn+d

формула суммы n членов: Sn=(а1 + аn)*n/2 или есть такая формула Sn=2а1+d(n-1)/2*n чаще всего используют первую формулу.

2) -2,-4,-6,-8... да является -2+(-2)=-4 так же -6+(-2)=-8 ты прибавляешь одно и тоже число

-13,-3,13,23... нет

4,7(16 оценок)

Это интересно:

Дом-и-сад

30.06.2021

Как повесить полку, не используя для этого гвозди...

Семейная-жизнь