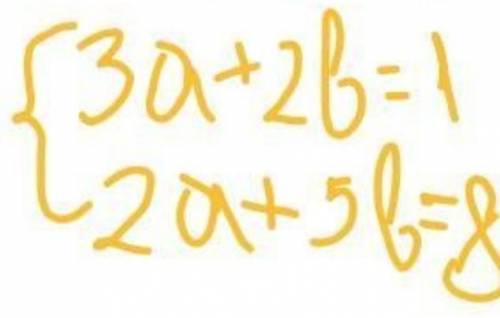
До обеда:
Объем работы 200 кустов
Производительность труда х кустов/час
Время работы ( 200/х ) часов
После обеда :
Объем работы 90 кустов
Производительность (х -20) кустов/час
Время работы 90/(х - 20) часов.
Зная, что на всю работу потрачено 7 часов, составим уравнение:
200/х + 90/(х -20) = 7
знаменатель не должен быть равен 0 :
х≠ 0 ; х≠ 20
избавимся от знаменателей, умножим обе части уравнения на х(х-20):
200(х-20) + 90х = 7х(х-20)
200х - 4000 + 90х = 7х² - 140х
290х - 4000 = 7х² - 140х
7х² - 140х - 290х + 4000 = 0
7х² - 430х + 4000 = 0
D = ( - 430)² - 4*7*4000 = 184900 - 112000 = 72900 = 270²
D>0
x₁ = ( - (-430) - 270)/(2*7) = (430 - 270)/14 = 160/14 = 80/7 = 11 ³/₇ не удовл. условию задачи ( т.к. < 20 )
х₂ = ( - (-430) +270)/(2*7) = (430 + 270)/14 = 700/14 = 50 (кустов/час)
Проверим:
200/50 + 90/(50 - 20) = 4 + 3 = 7 (часов)
ответ: по 50 кустов в час высаживала Валентина до обеда.
Вроде так. ( это у меня было написано в заметках, потому что мы тоже писали эту задачу, вот я и скопировала и вставила сюда).
2*sin2x*cos3x=0
sin2x=0 cos3x=0
2x=pi n 3x=pi/2+pi n
x=pi n/2 x=pi/6+pin/3
2)
Используем формулe приведения:cos(pi/2 -x) + cos3x = 0
По формуле преобразования суммы косинусов в произведение:
2cos(pi/4 +x)*cos(pi/4 -2x) = 0
Разбиваем на два уравнения:
cos(pi/4 +x) = 0 и cos(2x- pi/4)=0pi/4 +x = pi/2 + pi*k 2x- pi/4 = pi/2 +pi*nx = pi/4 + pik x = 3pi/8 + pi*n/2