. Любое число можно представить в виде произведения простых множителей. Запишем:
, где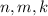 
- некоторые натуральные числа.
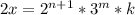является полным квадратом, значит 
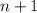и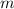 
- четные числа, а 
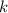- полный квадрат. Аналогично, число 
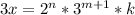является полным кубом, значит 
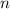и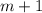 
делятся на 3, а 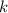- полный куб. 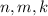это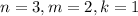 
, значит 
.
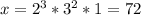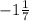
7; 8
Объяснение:
Пусть n и n+1 - последовательные натуральные числа,
тогда n(n+1) - их произведение, (n+1)²-n² - разность квадратов.
По условию задачи, произведение этих чисел на 41 больше разности их квадратов. Составляем уравнение:
n(n+1) - [(n+1)²-n²] = 41
n²+n-[n²+2n+1-n²] = 41
n²+n -[2n+1] = 41
n²+n-2n-1-41=0
n²-n-42=0
n₁*n₂ =-42 и n₁+n₂=1
n₁=7
n₂=-6 ∉ N
n=7
n+1=7+1=8