Відповідь:
Шість головних діагоналей дорівнюють подвоєній стороні шестикутника.
Шість додаткових діагоналей дорівнюють стороні шестикутника помноженій на корень квадратний із трьох.
Пояснення:
У правильному шестикутнику є шість головних діагоналей, що проходять крізь його геометричний центр ( центр описаної та вписаної окружності ), одна з них намальована синім кольором на малюнку. Довжина цієї діагоналі дорівнює подвоєній стороні шестикутника. Тому, що у правильному шестикутнику сторона дорівнює радіусу описаної окружності, а діагональ дорівнює двом радіусам.
Існує ще шість додадкових діагоналей, що не проходять крізь центр шестикутника, одна з таких діагоналей намальована червоним кольором на малюнку. Довжина такої діагоналі дорівнює стороні шестикутника помноженій на корень квадратний із трьох. Тому, що ця діагональ утворює рівнобічний трикутник з кутом при основі 30°, а основа трикутника дорівнює стороні шестикутника помноженій на 2 × cos (30°) = sqrt (3).
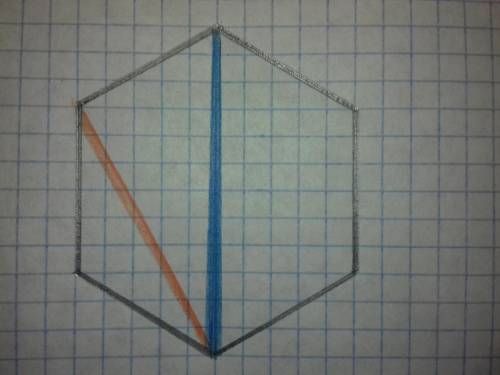
Диаграмма Венна (также используется название диаграмма Эйлера — Венна) — схематичное изображение всех возможных отношений (объединение, пересечение, разность, симметрическая разность) нескольких (часто — трёх) подмножеств универсального множества. На диаграммах Венна универсальное множество {\displaystyle U}U изображается множеством точек некоторого прямоугольника, в котором располагаются в виде кругов или других простых фигур все остальные рассматриваемые множества[1][2].
Диаграммы Венна применяются при решении задач вывода логических следствий из посылок, выразимых на языке формул классического исчисления высказываний и классического исчисления одноместных предикатов[3], для :
описания функционирования формальных нейронов Мак-Каллока и сетей из них[4]
синтеза надежных сетей из не вполне надежных элементов[5],
построения управляющих и самоуправляющихся систем и блочного анализа и синтеза сложных устройств[6],
получения логических следствий из заданной информации, минимизации формул исчислений[7][8].
Диаграммы Венна при {\displaystyle n}n фигур изображают все {\displaystyle 2^{n}}2^{n} комбинаций {\displaystyle n}n свойств, то есть конечную булеву алгебру[9]. При {\displaystyle n=3}n=3 диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
Дальнейшим развитием аппарата диаграмм Венна в классическом исчислении высказываний является аппарат вероятностных диаграмм [10], понятие сети диаграмм, использующей диаграммы Венна как операторы[11].
Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году.
Объяснение: