Сначала мы пишем систему и смотрим на коэффициенты при х и у.
В данном случае, особой разницы нет, поэтому останавливаемся на коэффициентах при х. В первом уравнении коэффициент при х равен 4, а во втором 3. Нам надо, чтобы при почленном сложении двух уравнений сумма коэффициентов при х равнялась нулю. Этого можно добиться искусственно, если первое уравнение домножить на 3, а второе уравнение домножить на (-4) (данная операция обозначена вертикальными "палочками", после которых стоит знак умножения на нужное нам число
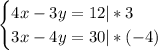
Получаем следующую систему:
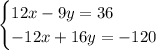
Теперь складываем уравнения "почленно", т.е. иксы с иксами, игреки с игреками, свободные члены со свободными членами. В результате получаем:
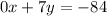
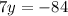
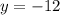
Осталось найти х. Для этого найденное значение у=-12 подставим в любое из первоначальных уравнений, например, в первое:
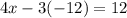

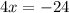

Осталось записать ответ. Допускаются следующие записи:
х=-6, у=-12 или (-6;-12)
Задание можно решить двумя
файл): через построение прямоугольного треугольника по имеющимся крайним точкам.Угол между касательной и положительным направлением оси ОХ(угол Д) -тупой,следовательно, коэффициент будет отрицательным.
файл) :найти координаты двух данных точек,подставить их в уравнение прямой(в линейное уравнение) у = kx+b ,вычесть одно уравнение из другого и найти коэффициент.
3 .Треугольник можно строить не только по крайним точкам,но и по углу треугольника между положительными значениями оси ОХ и ОУ,если так выходит треугольник с целыми клетками(необязательно,надо делать как удобнее и как учили).