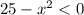
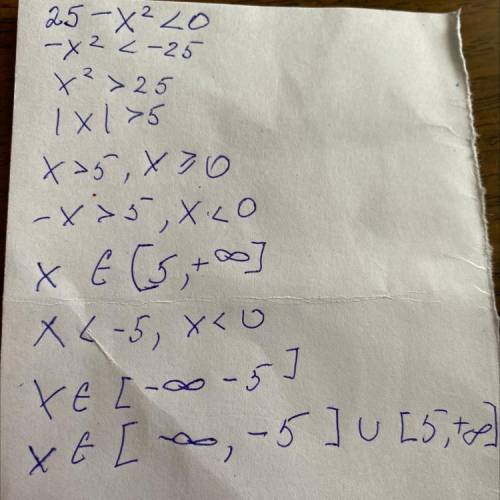
Объяснение:
-х²+25<0
х²-25>0
(х-5)(х+5)>0
Это парабола ветками вверх, поэтому на интервале от (-5;5) меньше 0, а на интервале от (-беск;-5)U(5;+беск) функция больше 0. ответ: хє(-беск;-5)U(5;+беск)
a) (2x - y)(x + 2y) = -3
1) 2x - y = 3 => y = 2x - 3
x + 2y = -1 => x + 2(2x - 3) = - 1 =>
x + 4x - 6 = -1 => 5x = 5 => x = 1
y = 2x - 3 = 2 - 3 = -1.
Первое решение (x, y) = (1, -1)
2) 2x - y = - 3 => y = 2x + 3
x + 2y = 1 => x +2(2x + 3) = 1 =>
x + 4x + 6 = 1 => 5x = - 5 => x = -1
y = 2x + 3 = -2 + 3 = 1.
Второе решение (x, y) = (-1, 1)
3) 2x - y = 1 => y = 2x - 1
x + 2y = -3 => x + 2(2x - 1) = -3 =>
x + 4x - 2 = -3 => 5x = -1 => x = - 1/5 - нецелое.
4) 2x - y = -1 => y = 2x + 1
x + 2y = 3 => x + 2(2x + 1) = 3 =>
x + 4x + 2 = 3 => 5x = 1 => x = 1/5 - нецелое.
Всего два решения (x, y) = (1, -1) и (x, y) = (-1, 1)
б) 2x² + xy - y² = -3
x² - y² + x² + xy = -3
(x - y)(x + y) + x(x + y) = -3
(x + y)(x - y + x) = -3
(x + y)(2x - y) = -3
1) x + y = 3 => y = 3 - x
2x - y = -1 => 2x - 3 + x = -1 =>
3x - 3 = -1 => 3x = 2 => x = 2/3 - нецелое
2) x + y = 1 => y = 1 - x
2x - y = -3 => 2x - 1 + x = -3 =>
3x -1 = -3 => 3x = -2 => x = -2/3 - нецелое
3) x + y = -3 => y = -3 - x
2x - y = 1 => 2x +3 + x = 1 =>
3x + 3 = 1 = 3x = -2 => x = -2/3 - нецелое
4) x + y = -1 = y = -1 - x
2x - y = 3 => 2x +1 + x = 3 =>
3x + 1 = 3 => 3x = 2 => x = 2/3 - нецелое.
Второе уравнение не имеет решений в целых числах.
Написать уравнение плоскости проходящей через точки P(1,1,-2) и Q(3,-2,-1) и перпендикулярной плоскости 4x-2y-z-3=0.
Если дано уравнение плоскости, то известна нормаль N к этой плоскости: N = (4; -2; -1).
Для искомой плоскости нормаль N будет параллельным вектором n.
Точки P(1,1,-2) и Q(3,-2,-1) .
Вектор PQ = ((3-1=2; -2-1=-3; -1-(-2)=1) = (2; -3; 1).
Составим уравнение плоскости П как плоскости, проходящей через точку Р(1,1,-2) параллельно векторам →PQ (2; −3; 1) и →n = (4; -2; -1).
x - 1 y - 1 z + 2 x - 1 y - 1
2 -3 1 2 -3
4 -2 -1 4 -2
∆ = a11 a12 a13 a11 a12
a21 a22 a23 a21 a22
a31 a32 a33 a31 a32
= a11•a22•a33 + a12•a23•a31 + a13•a21•a32 - a13•a22•a31 - a11•a23•a32 - a12•a21•a33
∆ = (x - 1)*(-3)*(-1) + (y - 1)*1*4 + (z + 2)*2*(-2) - (z + 2)*(-3)*4 - (x - 1)*1*(-2) - (y - 1)*2*(-1) = 4x - 4 + 4y - 4 - 4z - 8 + 12z + 24 + 2x - 2 + 2y - 2 = 6x + 6y + 8z + 4 = 0.
Или, сократив на 2, получаем искомое уравнение плоскости:
3x + 3y + 4z + 2 = 0.