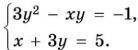
Пусть искомый год XYZT (1000*X+100*Y+10*Z+T, X,Y,Z,T - цифры). Можно составить систему:
X+Y+Z+T=21
1000*X+100*Y+10*Z+T+5355=1000*T+100*Z+10*Y+X
и дальше долго решать, и получить кучу странных ответов
Пойдем чуть по другому.
Очевидно, год рождения - четырехзначное число, притом первая цифра равна 1.
Тогда последняя цифра равна 6 (эта цифра + 5 = 11).
Итак, год рождения теперь выглядит 1..6.
Теперь уже можно написать уравнение - пусть год 1XY6.
Тогда X+Y=21-1-6=14; 1000+100X+10Y+6+5355=6000+100Y+10X+1
X+Y=14; Y-X=4
Складываем оба уравнения, получим 2Y=18, откуда Y=9. Тогда X=14-9=5.
ответ: 1596.
В 1596 году, например, родился Рене Декарт.
P.S. А если предположить, что в будущем возможны путешествия во времени и некто из будущего построил науку нового времени, то вариантов несколько больше - всего 4:
1596
2487
3378
4269
Пусть - четырехзначное число, записанное одинаковыми цифрами (х = 1, 2, ...9)
Тогда на четных местах: х+х = 2х, на нечетных местах: х+х = 2х. суммы одинаковые, значит делится на 11.
2) ххх - трехзначное число, записаноое одинаковыми цифрами (х = 1, 2,...9).
На четных местах: х, на нечетных местах: х+х = 2х. 2х ≠ х, значит число ххх на 11 не делится.
Число делится на 37 тогда и только тогда, когда на 37 делится модуль утроенного числа сотен, сложенного с учетверённым числом десятков, за вычетом числа единиц, умноженного на семь.
|3x + 4x - 7x| = |0| = 0 - делится на любое число, в т.ч. и на 37.