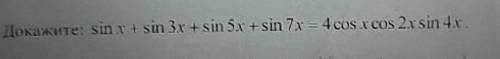
Пусть 1 число - x
Пусть 2 число y
Составим систему. на основе условия
{x+y=13
{xy=36
Выразим из 1 x и подставим во 2
x=13-y
(13-y)y=36
13y-y^2-36=0;
y^2-13y+36=0
D=169-144=25
x1=13+5/2=9;
x2=13-5/2=8/5;
И так, у нас 2 варианта чисел, проверим их, на найдем лишнее, подстановкой в оба уравнения
1) {9+y=13
{9y=36
{y=13-9
{y= 4
Подходит. Так как число может быть только одним, то второе значение x - неподходит
ответ: эти числа 9 и 4
Пусть 1 число - x
Пусть 2 число y
Составим систему. на основе условия
{x+y=13
{xy=36
Выразим из 1 x и подставим во 2
x=13-y
(13-y)y=36
13y-y^2-36=0;
y^2-13y+36=0
D=169-144=25
x1=13+5/2=9;
x2=13-5/2=8/5;
И так, у нас 2 варианта чисел, проверим их, на найдем лишнее, подстановкой в оба уравнения
1) {9+y=13
{9y=36
{y=13-9
{y= 4
Подходит. Так как число может быть только одним, то второе значение x - неподходит
ответ: эти числа 9 и 4
Объяснение:
Проведем доказательство тождества следующим образом:
- проведем равносильные преобразования левой части доказываемого тождества;
- если в итоге преобразований левая часть примет ту же форму что и правая часть - тождество доказано.
Итак - левая часть:
Сгруппируем следующим образом:
Воспользуемся формулой суммы синусов:
Поочередно сложим группы внутри скобок:
Тогда вся левая часть примет вид:
для преобразования суммы косинусов в скобках воспользуемся такой формулой:
Выражение примет вид:
В результате преобразований левая часть приняла тот же вид что и правая.
Тождество доказано.