Вообще область значений тангенса и котангенса - все действительные числа:
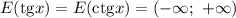
а)
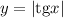
Если рассмотреть модуль тангенса, то отрицательные значения примут противоположные значения, то есть станут положительными. Нулевое и положительные значения сохранятся. Получим область значений:
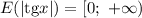
б)
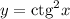
Котангенс может принять значение любого действительного числа, но при возведении любого числа в квадрат результат получится неотрицательным.
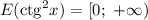
в)
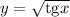
Тангенс может принять значение любого действительного числа. Под знак корня из них можно записать любое неотрицательное, при этом в результате может получиться любое неотрицательное число.
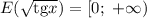
г)
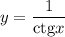
Котангенс может принять значение любого действительного числа. При делении 1 на любое число (отличное от нуля) может получиться любое число, кроме нуля.
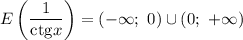
a2 = 3pi/4+2pi*k; cos a2 = -√2/2
cos(60 + a1) = cos 60*cos a1 - sin 60*sin a1 =
= 1/2*√2/2 - √3/2*√2/2 = √2/4*(1 - √3) = -√2(√3 - 1)/4
cos(60 + a2) = cos 60*cos a2 - sin 60*sin a2 =
= -1/2*√2/2 - √3/2*√2/2 = -√2/4*(1 + √3) = -√2(√3 + 1)/4
2) sin a = 2/3; cos b = -3/4; a ∈ (pi/2; pi); b ∈ (pi; 3pi/2)
cos a < 0; sin^2 a = 4/9; cos^2 a = 1-4/9 = 5/9; cos a = -√5/3
sin b < 0; cos^2 b = 9/16; sin^2 b = 1-9/16 = 7/16; sin b = -√7/4
sin(a+b) = sin a*cos b + cos a*sin b =
= 2/3*(-3/4) + (-√5/3)(-√7/4) = -6/12 + √35/12 = (√35 - 6)/12
cos(-b) = cos b = -3/4