Определим общее число расстановок на пяти позициях 5 шариков:
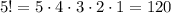
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах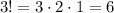 
Таким образом, всего имеется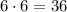 
недопустимых расстановок.
Значит, допустимых расстановок имеется:
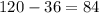
ответ: 84
:
(С ФСУ)
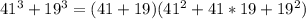
Выражение делится на число тогда, когда один из множителей делится на число
41 + 19 = 60, 60 делится на 60, следовательно и сумма будет делится
:
(Более замороченный)
Для этого можно просто доказать кратность этого выражения на множители числа 60.
60 =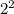 
* 3 * 5
41, при делении на 5, дает остаток 1 (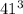
так же будет давать этот остаток)
19, при делении на 5, дает остаток 4 (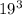
так же будет давать этот остаток)
1 + 4 = 5 : 5
Сумма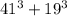 
будет делится на 4 ( по признаку деления на 4, сумма будет оканчиваться на 0)
А деление на 3 можно доказать суммой цифр, 4+1 = 5 (остаток, при делении на 3, 2), 1 + 9 = 10 (остаток, при делении на 3, 1)
1 + 2 = 3 : 3
чтд
1) -100
Пояснення:
2-102 = -100
Объяснение: