
y=x(x+2)-6x при x≥0
y=(-x)(x+2)-6x при x<0
y=x2+2x-6x при x≥0
y=-x2-2x-6x при x<0
y=x2-4x при x≥0
y=-x2-8x при x<0
1) y=x2-4x, при x≥0
Графиком подфункции - парабола.
Ветви направлены вверх.
x^2-4x=0
x(x-4)=0
x1=0 x-4=0
x2=4
2) y=-x2-8x, при x<0
График подфункции - парабола.
Ветви направлены вниз
-x2-8x=0
-x(x+8)=0
x1=0
x+8=0
x2=-8
Первый график у нас получается y=x2-4x, при x≥0
Второй график: y=-x2-8x, при x<0
Прямая: y=m
Две точки пересечения будет только когда прямая будет касаться вершин парабол.
Найдем координату Y вершин парабол, это и будут m, при которых прямая y=m будет иметь только две точки пересечения с графиком.
1) Для первой подфункции x0=-b/(2a)=-(-4)/(2*1)=4/2=2
y0=-5,25
2) Для второй подфункции x0=-b/(2a)=-(-8)/(2*(-1))=8/(-2)=-4
y0=(-4)2-8*(-4)=24
ответ: m1=-5,25, m2=24
вроде так!
f(x) = 5 +2x - 3
f(x) = 2x + 2
Есть несколько начертить этот график, но в конечном итоге получается одно и то же. Мне больше нравится этот:
1) Строим график функции f(x) = x. Это будет прямая, построенная под углом 45° к оси Ох (пунктирная линия на графике)
2) Теперь строим график функции f(x) = 2x путём сжатия исходного графика к оси Оу. Выглядит это так (прямая, выходящая из начала координат, которая не пунктирная).
3) Ну и наконец, смещаем полученный график на 2 единицы вверх (прямая, выходящая из точки 2 на оси Оу, самая тёмная на рисунке)
Когда разберётесь с этим, можно опускать эти пункты и сразу строить конечный, но на первых порах лучше максимально разобрать этот процесс
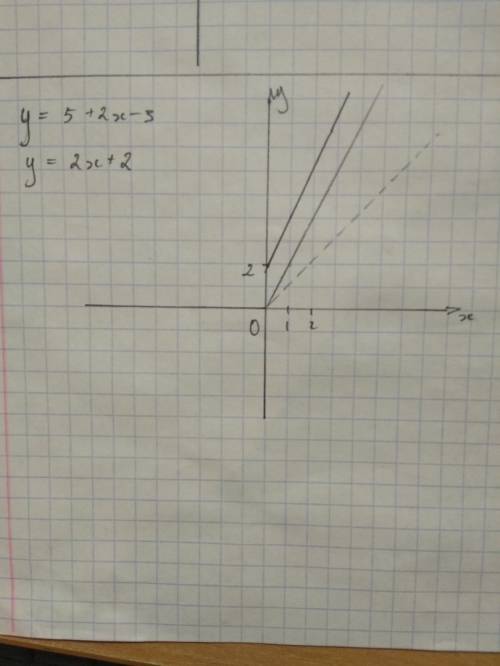
f(x) = 5 +2x - 3
f(x) = 2x + 2
Есть несколько начертить этот график, но в конечном итоге получается одно и то же. Мне больше нравится этот:
1) Строим график функции f(x) = x. Это будет прямая, построенная под углом 45° к оси Ох (пунктирная линия на графике)
2) Теперь строим график функции f(x) = 2x путём сжатия исходного графика к оси Оу. Выглядит это так (прямая, выходящая из начала координат, которая не пунктирная).
3) Ну и наконец, смещаем полученный график на 2 единицы вверх (прямая, выходящая из точки 2 на оси Оу, самая тёмная на рисунке)
Когда разберётесь с этим, можно опускать эти пункты и сразу строить конечный, но на первых порах лучше максимально разобрать этот процесс
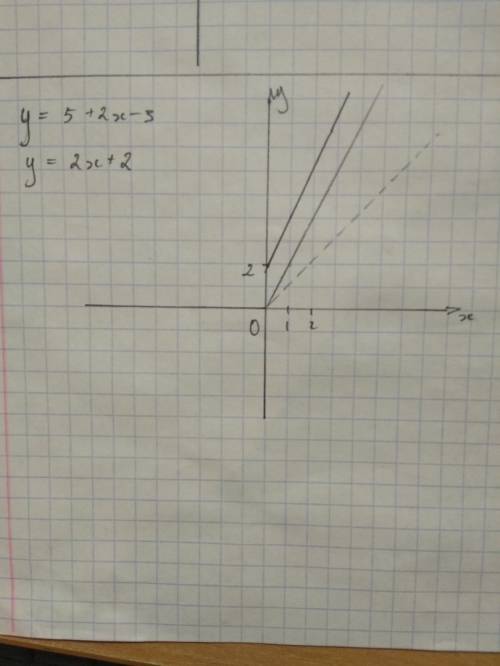
Решение задания прилагаю