Большое количество задач такого типа решаются при формулы Ньютона-Лейбница:
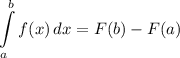
Поэтому, во-первых, нужно найти  и
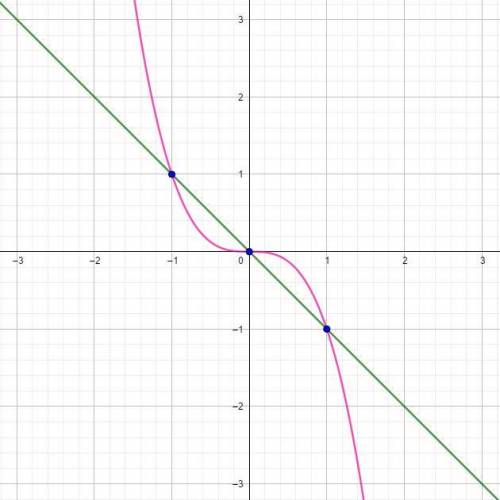
и 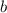 - абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:
- абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:
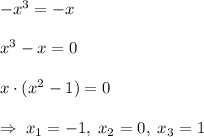
А так как есть целых три точки пересечения, то придется считать два интеграла: первый - от 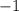 до
до 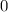 (как результат приравнивания функций:
(как результат приравнивания функций: 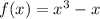 ), а второй - от
), а второй - от 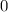 до
до  (здесь уже
(здесь уже 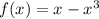 ):
):
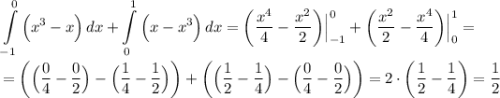
Значит, площадь искомой фигуры (состоящей из нескольких других фигур) равна 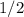 или
или 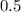 (каких-то квадратных единиц измерения), если перевести в десятичную дробь.
(каких-то квадратных единиц измерения), если перевести в десятичную дробь.
ответ:: S6 = 10,2
Объяснение:
1. Для определения суммы шести членов арифметической прогрессии необходимо узнать значение шестого ее члена и только тогда найти S6 по формуле
Sn = (a1 + an) : 2 * n.
2. Известна формула для энного члена арифметической прогрессии
аn = a1 + d *(n - 1).
3. Пользуясь этой формулой вычислим разность прогрессии d.
a4 = a1 + d * 3;
1,8 = 1,2 + 3 d;
d = (1,8 - 1,2) : 3 = 0,6 : 3 = 0,2.
4. Теперь найдем а6.
а6 = а1 + d * 5 = 1,2 + 0,2 * 5 = 1,2 + 1 = 2,2.
5. Отвечаем на во задачи
S6 = (a1 + a6) : 2 * 6 = (1,2 + 2,2) : 2 * 6 = 10,2.