0,404
Объяснение:
Пусть H₀ - вероятность отказа обеих микросхем.
Р(H₀)=0,07*0,1=0,007
Пусть Н₁ - вероятность отказа первой микросхемы при условии работо второй.
Вторая микросхема работает с вероятностью 1-0,1=0,9.
Р(Н₁)=0,07*0,9=0,063
Пусть Н₂ - вероятность отказа второй микросхемы при условии работо первой.
Первая микросхема работает с вероятностью 1-0,07=0,93.
Р(Н₂)=0,1*0,93=0,093.
Вероятность Н₃ работы обеих микросхем равна
P(Н₃)=0,9*0,93=0,837.
Вероятность отказа одной из микросхем (любой)
Р(Н₁)+Р(Н₂)=0,063+0,093=0,156.
Значит при условии отказа одной из микросхем (любой) это будет первая микросхема выражается отношением
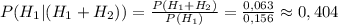
0,404
Объяснение:
Пусть H₀ - вероятность отказа обеих микросхем.
Р(H₀)=0,07*0,1=0,007
Пусть Н₁ - вероятность отказа первой микросхемы при условии работо второй.
Вторая микросхема работает с вероятностью 1-0,1=0,9.
Р(Н₁)=0,07*0,9=0,063
Пусть Н₂ - вероятность отказа второй микросхемы при условии работо первой.
Первая микросхема работает с вероятностью 1-0,07=0,93.
Р(Н₂)=0,1*0,93=0,093.
Вероятность Н₃ работы обеих микросхем равна
P(Н₃)=0,9*0,93=0,837.
Вероятность отказа одной из микросхем (любой)
Р(Н₁)+Р(Н₂)=0,063+0,093=0,156.
Значит при условии отказа одной из микросхем (любой) это будет первая микросхема выражается отношением
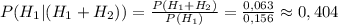
2) При p<0 левая часть задает параболу, ветви которой направлены вниз, поэтому она не лежит целиком в верхней полуплоскости, значит такие p нам не подходят.
3) При p>0 левая часть задает параболу, ветви которой направлены вверх, поэтому неравенство будет выполняться при любом х в случае, когда эта парабола не пересекает ось Ох, т.е. левая часть не имеет корней или, что то же самое,. ее дискриминант отрицателен:
D=(2p-3)²-4p(p+3)=4p²-12p+9-4p²-12p=-24p+9<0,
откуда p>9/24=3/8.
ответ: p∈(3/8;+∞).