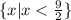Объяснение:
Задача №2.
Чтобы определить, принадлежит ли точка графику, надо подставить в формулу значения иксов и игриков:
y = -4x + 3
-115 = -4*(-28)+3
-115 не равно 115 - точка A графику не принадлежит.
Подставляем данные точки B:
-53 = -4 * 14 + 3
-53 = -53 - точка B принадлежит графику, так как результаты вычислений совпали.
Задача №3.
Если график линейной функции y = kx+b проходит через начало координат, то он проходит через точку 0 по иксу и 0 по ординате.
Следовательно, график принимает вид y = kx.
ответ: y = -4x
А если график параллелен, то получается просто число, без иксов, без ничего. ответ: y = -4
ответ: Запись в виде интервала: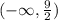
Нотация построения множества: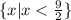
Объяснение: Положим аргумент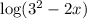
больше 0, чтобы выяснить, где определено данное выражение.
Решим относительно x.
Возведем 3 в степень 2.
Вычтем 9 из обеих частей неравенства.
Разделим каждый член на -2 и упростим.
Разделим каждый член в выражении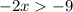
на -2. При умножении или делении обеих частей неравенства на отрицательное значение, знак неравенства меняется на противоположный.
Сократим общий множитель -2.
Деление двух отрицательных значений дает положительный результат.
Решение включает все истинные интервалы.
Областью определения являются все значения x, которые делают выражение определенным.
Запись в виде интервала: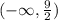
Нотация построения множества: