Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
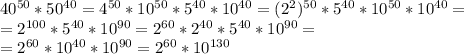
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
Через вершину C прямоугольника ABCD проведена прямая, параллельная диагонали BD и пересекающая прямую AB в точке M. Через точку M проведена прямая, параллельная диагонали AC и пересекающая прямую BC в точке N. Найдите периметр четырехугольника ACMN, если диагональ BD равна 8 см
–––––––––––––––
Казалось бы очевидно- стороны четырехугольника ACMN равны между собой и равны диагоналям прямоугольника. Тем не менее это нужно доказать.
МС║ВD по построению.
АВ║ СD - стороны прямоугольника, след, ВМ║СD
Противоположные стороны четырехугольника МВСД лежат на параллельных прямых. ⇒
МВДС - параллелограмм.⇒
ВМ=СD. Но СD=АВ ⇒ ВМ=АВ.
СN ⊥ АМ и делит ее пополам. СВ - высота и медиана ∆ АСМ,⇒
∆ АСМ равнобедренный, и СВ его биссектриса.
В ∆ АМN отрезок NB – медиана и высота ⇒
∆ МАN равнобедренный, и BN- его биссектриса.
AN= MN, a MN=MC=AC
∠АМN =∠MАС как накрестлежащие при параллельных МN и АC и секущей АМ.
Но углы равнобедренного ∆ САМ при АМ равны.⇒∠ АМN=∠СМА=∠САМ ,
МВ ⊥ СN⇒ является высотой ∆ NMC и оо равенству углов при М - биссектрисой. ⇒
NMC - равнобедренный, и NM=MC, отсюда следует равенство AN=MN=MC=АС
Четырехугольник АСМN- ромб.
АС- диагональ прямоугольника ABCD и по условию равна 8
Периметр АСМN=8*4=32