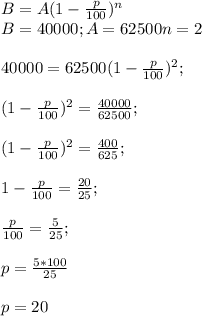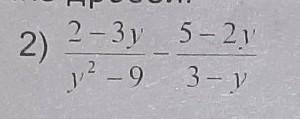
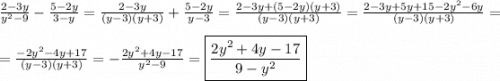
а)2sin²x-3sinx-2=0
Замена sinx=t
2t²-3t-2=0
D=3²+4×2×2=25
t₁= 3+√D÷4=3+5÷ 4=8÷4=2
t₂=3-√D÷4=3-5÷4=-2÷4=-0,5
Возвращаемся к замене
sinx=2 sinx=-0,5
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z
4cos²x+4sinx-1=0
cos²x=1-sin²x
4( 1-sin²x)+4sinx-1=0
4-4sin²x+4sinx-1=0
-4sin²x+4sinx-1+4=0
-4 sin²x+4sinx+3=0 ÷(-1)
4sin²x-4sinx-3=0
Замена sinx=t
4t²-4t-3=0
D=4²+4×4×3=16+48=64
t₁=4+√D÷8= 4+8÷8=12÷8=1,5
t₂=4-√D÷8=4-8÷8= -4÷8=-0,5
Возвращаемся к замене
sinx=1,5 sinx=-1\2
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z
20%
Объяснение:
Пусть ежегодно цена понижалась на x% . Тогда в первый раз цена понизится на 62500*0,01x= 625x рублей и станет (62500 - 625x)руб .
(62500 - 625x)*0.01 x = 625x - 6,25x^2 - второе понижение
62500-625x - (625x-6,25x^2) = 62500 -1250x+6,25x^2 - цена после второго понижения. Так как по условия цена после второго понижения 40000 рублей. то составляем уравнение:
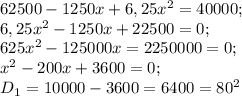
x=20 или x= 180 -не удовлетворяет условию задачи.
Поэтому ежегодно цена уменьшалась на 20%.
Воспользуемся формулой сложных процентов