
1) 360:60=6° проходит минутная стрелка за 1 минуту
2) 360:12:60=0,5° проходит часовая стрелка за 1 минуту
Если рассмотреть угол, который пройдут стрелки с 8 часов. Пусть этот угол равен х°, значит угол который минутная стрелка 6х, а часовая за это время. Поскольку мы находим положение минутной стрелки,то найдем сразу какой угол был между часовой и минутной стрелки в 8:00 (8*360:12=240°). Поскольку часовая и минутная стрелка совпали, то они одинаковое количество градусов.
6х=0,5х+240
6-0,5х=240
5,5х=240
х=240:5,5=480/11=43 7/11 минуты
Значит Петя ушел в школу, когда время на часах было 8 часов 43 7/11 минуты.
Следующее условие Петя пришел, когда стрелки на часах были в противоположных направлениях, значит угол между ними был 180°. Следовательно минутная стрелка была на 9 часах, или 45 минутах.
По приблизительной прикидки: 2 ч 45 минут.
Если считать время точно:
По аналогии с предыдущими расчетами.
Найдем для начала угол который был в 2 часа дня между часами:
2*360:12=60° начальный угол между стрелками.
Часовая стрелка х, а минутная стрелка 6х, с учетом конечного положения стрелок 180°.
60°+0,5х=6х-180°
6х-0,5х=180+60
5,5х=240
х=240:5,5
х=43 7/11 минуты
Значит Петя пришел домой в 2 ч 43 7/11 минуты дня, или 14 ч 43 7/11 минуты.
14 ч 43 7/11 мин - 8 ч 43 7/11 минуты =6 ч отсутствовал Петя дома
ответ 6 часов
По грубой прикидки:
14 ч 45 мин-8ч 45 мин=6 ч разница.
1)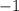 ,
, 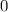 ,
,  .
.
2)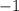 ,
, 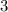 .
.
Объяснение:
1) По утверждению, обратному лемме Ферма, в точке экстремума функции значение её производной равно нулю. Отсюда следует, что для нахождения точки экстремума функции следует сначала найти производную функции, а затем найти точки, в которых она равна нулю. Они и будут являться точками экстремума исходной функции.
Для данной функции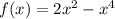 найдём производную:
найдём производную:
Решим теперь уравнение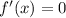 :
:
Отсюда следует, что или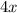 равно нулю, или
равно нулю, или 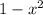 равно нулю.
равно нулю.
Первое:
Второе:
Получается, что точками экстремума функции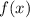 являются
являются 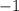 ,
, 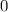 и
и  .
.
2) Аналогично первому заданию, для данной функции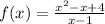 найдём производную:
найдём производную:
Решим теперь уравнение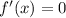 :
:
Из него следует, что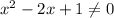 , а также
, а также 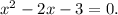
Для первого:
Для второго:
Все удовлетворяют условию
удовлетворяют условию 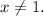
Получается, что точками экстремума функции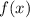 являются
являются 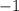 и
и 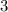 .
.