Нюше нужен уникальный набор: ручка + карандаш + тетрадь! И она в нужном месте! Каждый товар в этом магазине уникален!
Это задача на классическое правило умножения: Если объект можно выбрать и если после каждого такого выбора объект можно выбрать то выбор пары в указанном порядке можно осуществить
------------------------------------------------ Нужно последовательно одно за другим осуществить три действия (в любом порядке): выбор КАРАНДАША, выбор РУЧКИ, выбор ТЕТРАДИ.
Пусть сначала выбирается карандаш, потом ручка, потом тетрадь: - первое действие можно осуществить И ПРИ ЛЮБОМ ЕГО ОСУЩЕСТВЛЕНИЯ второе действие можно осуществить и в конце ПРИ ЛЮБОМ ОСУЩЕСТВЛЕНИЯ ПЕРВЫХ ДВУХ ДЕЙСТВИЙ третье действие можно осуществить
можно выбрать 
и если после каждого такого выбора объект 
можно выбрать 
то выбор пары 
в указанном порядке можно осуществить 
Пояснение:
1) Если максимально просто объяснять, то когда одинаковые значения , а степени могут быть одинаковые или разные , умножаются , например как тут:
2) А при делении наоборот степени вычитаются, например :
3) Есть ещё 1 пример, это когда имеется степень за скобкой, типа
, то тут степени умножаются друг на друга и у нас выйдет так:
Теперь решение:
Задача состоит в том, чтобы вместо точек подставить такое значение со степенью, чтобы получилось равенство.
1)
- такие действия буду пропускать, как раз потренируешься.
2)
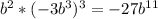
3)
4)
5)
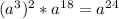
Если посмотришь на свойства степеней, то узнаешь ещё больше , чтобы быть всегда на готове.