х³-5х²-2х+24=0 Корни уравнения надо искать среди делителей свободного слагаемого. Делители числа 24: 1;2;3;4;6;12;24 -1;-2;-3;-4;-6;-12;-24 Проверкой убеждаемся, что х=2 - корень уравнения В самом деле. (-2)³-5·(-2)²-2·(-2)+24=0 -8-20+4+24=0 -28+28=0 - верно. Значит, левая часть раскладывается на множители, один из которых (х-(-2))=х+2 Делим -х³-5х²-2х+24 | x+2 x³+2x² x²-7x+12
_-7x²-2x+24 -7x²-14x
_12x+24 12x+24
0
х³-5х²-2х+24=0 (x+2)(x²-7x+12)=0 x+2=0 или х²-7х+12=0 х=-2 х=(7-1)/2=3 или х=(7+1)/2=4 О т в е т. -2; 3; 4.
t≤2, t≥3
Объяснение:
все выражение находится под корнем. Корень имеет смысл, когда подкоренное выражение больше или равно нулю:
t²-5t+6≥0
найдем корни квадратного трехчлена, для этого приравняем его к нулю:
t²-5t+6=0
по теореме Виета: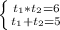
, откуда корни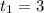 
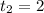
отметим точки на прямой (рис) (закрашенными, т.к наше неравенство нестрогое)
знаки начинаются с +, дальше чередуем.
у нас ≥, выбираем +
t ∈ (-∞; 2] ∪ [3; +∞), что можно понимать, как: нас устраивает t меньше 2 и 2 включительно и больше 3, включая 3 => t≤2, t≥3