Серед наведених тверджень:
A - множина розв'язків нерівності х² ≥ 4.
B - область визначення функції y = √x-3.
Правильне твердження:
A) A - множина розв'язків нерівності х² ≥ 4.
Пояснення:
A) Множина розв'язків нерівності х² ≥ 4 включає всі значення х, які задовольняють умові х² ≥ 4. Це означає, що х може бути будь-яким числом, що не менше -2 або не більше 2. Таким чином, множина розв'язків цієї нерівності є A = {x | x ≤ -2 або x ≥ 2}.
B) Область визначення функції y = √x-3 визначається умовою, що підкореневий вираз повинен бути не менше 0, тобто x - 3 ≥ 0. З цієї умови випливає, що x ≥ 3. Таким чином, область визначення функції складає B = {x | x ≥ 3}.
Отже, правильне твердження - A) множина розв'язків нерівності х² ≥ 4.
поставь найкраща відповідь
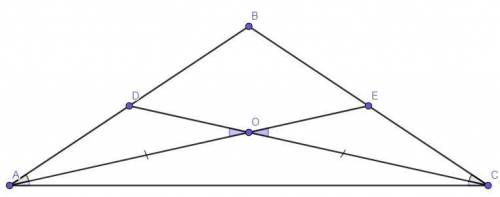
Дано :
ΔАВС - равнобедренный (АВ = ВС).
D ∈ AB, Е ∈ ВС.
АЕ ∩ CD = О.
∠ACD = ∠CAE.
Доказать :
AD = CE.
Доказательство :
Рассмотрим ΔАОС.
Если в треугольнике два угла равны, то он - равнобедренный.Следовательно, ΔАОС - равнобедренный. Причём АО = ОС (боковые стороны), так как лежат против равных углов в одном треугольнике.
Рассмотрим ΔАВС.
В равнобедренном треугольнике углы при основании равны.Так как ΔАВС - равнобедренный (по условию), то ∠А = ∠С.
Тогда -
∠А = ∠DAO + ∠CAE
∠C = ∠ECO + ∠ACD
Учитывая равенство ∠ACD = ∠CAE и ∠А = ∠С, получаем, что ∠DAO = ∠ECO.
Рассмотрим ΔDOA и ΔEOC.
∠DOA = ∠EOC как вертикальные
∠DAO = ∠ECO по выше сказанному
АО = ОС по выше сказанному
Тогда ΔDOA = ΔEOC по стороне и двум прилежащим к ней углам (второй признак равенства треугольников).
В равных треугольниках против равных углов лежат равные стороны.Так как ∠DOA = ∠EOC, то по выше сказанному AD = CE.
Что требовалось доказать.
второе. 9:9+9 или 9:9+8
третье. 3:3+3 или 3:3+2
четвертое. 1:1+1 или 1:1