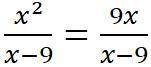
Смотрите фотографию
Объяснение:
4х⁴+х²-3=0
сделаем замену переменных
х²=y тогда х⁴=у²
получим уравнение
4y²+y-3=0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 1² - 4·4·(-3) = 1 + 48 = 49
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
y₁ = (-1 - √49)/ 2·4 = ( -1 - 7)/ 8 = -8 /8 = -1
y₂ = (-1 + √49)/ 2·4 = ( -1 + 7)/ 8 = 6/ 8 = 0.75
1) y=-1 x²=-1 x=±√-1 x=±i это комплексные корни
х₁=√-1=i
x²=-√-1=-i
2) y=0.75=3/4
x²=3/4
x=±√(3/4)=±(√3)/2 это действительные корни
x₃= (√3)/2
x₄= -(√3)/2
4x^4+x-3=0
пусть у=(х+1)
4*(y-1)^4+y-4=0
4*((y-1)^4-1)+y=0
4*((y-1)^2-1)(y-1)^2+1)+y=0
4*y*(y-2)*((y-1)^2+1)+y=0
Один корень у=0 (х=-1)
иначе 4(у-2)*((y-1)^2+1)=-1
Вернемся к исходным обозначениям
(1-х)(x^2+1)=1/4
кубическое уравнение. один действительный корень (примерно 0,8556). В школе такие не решают. Хотел убрать решение, но оставил. Может пригодится.
Теперь вижу, что Вы в комментарии исправили условие .
4x^4+x^2-3=0
Тогда все просто у=х^2
4y^2+y-3=0
По теореме Виета:
корни у=-1 и у=3/4
Нас интересует только неотрицательный корень
у=3/4. Два решения х=sqrt(3)/2 или х=-sqrt(3)/2
х=0
Объяснение:
1. Найдём ОДЗ: х≠9
2. Отбросим знаменатели, они одинаковые. Получим: х²=9х
3. Переносим неизвестную в левую часть и меняем ее знак: х²-9х=0
4. Выносим общий множитель за скобки: х(х-9)=0
5. Когда произведение равно 0, то один из множителей равен 0:
х=0
х-9=0⇔х=9
6. ОДЗ не пропускает 9, значит х=0