
ответ:
ответ: 2 км/ч.
объяснение:
решение:
пусть скорость плота х км/ч,учитываем,что скорость плота равна скорости течения реки,тогда по течению скорость лодки равна (8 + х) км/ч, а против течения (8 - х) км/ч.
составим уравнение:
15/(8+x)+ 6/(8-x)=5/x;
(120-15х+48+6х)/(64+х²)=5/x;
(168-9x)/(64+x²)-5/x=0;
(168x-9x²-320+5x²)/(64х+х³)=0;
168x-9x²-320+5x²=0;
-4x²+168x-320=0;
сокращаем на -4:
x²-42x+80=0;
d=b²-4×a×c
d=(-42²)-4×1×80 = 1764-320=1444
d> 0, 2 корня
х₁=42+√1444/2×1 =42+38/2=80/2=40 (км/ч)---не подходит(так как плот не может плыть быстрее лодки, значит х=40 не является решением);
х₂=42-√1444/2×1=42-38/2=4/2=2 -(км/ч)---скорость течения реки;
ответ: 2 км/ч.
Если D = 0, то уравнение имеет один корень; x = -b / 2a, где b - это число, с x, a - число с x^2
Если D > 0, то уравнение имеет два корня; x1,2 =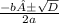 // там не должно быть буквы А, просто ± по-другому не ставился
// там не должно быть буквы А, просто ± по-другому не ставился
D = b^2 - 4ac = 10^2 - 4*3*3 = 64
Корень из 64 = 8
x1,2 = (-10 ± 8) / 2*3
x1 = - 1 / 3
x2 = -3
Объяснение: