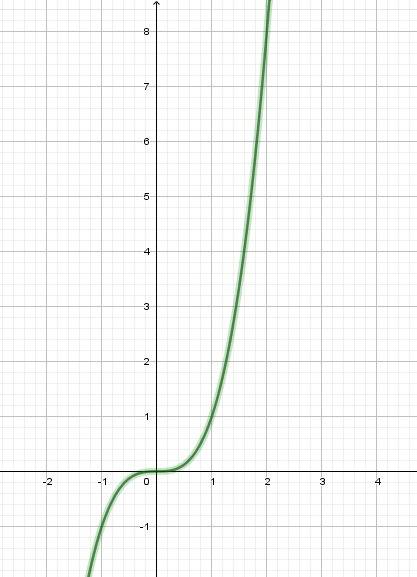
Точки построения графика: (0;0), (±1; ±1), (±2; ±8). График является нечетной.
Подставим координаты точки A(-5;125) в график уравнения, получим
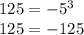
Поскольку равенство не верно, то график функции y = x³ не проходит через точку A(-5;125), т.е. точка не принадлежит графику y = x³
Подставим теперь координаты точки B(4;64), получим
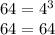
Поскольку равенство тождественно выполняется, то точка B принадлежит графику функции y = x³.
Подставим координаты точки C(-3;-27), имеем
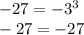
Раз равенство тождественно выполняется, то точка C(-3;-27) принадлежит графику функции y = x³
1) OA = OC = OB = a
Треугольники ОАВ, ОАС и ОВС - прямоугольные с равными катетами, значит они равны по двум катетам. Значит, равны и их гипотенузы:
АВ = АС = ВС.
Треугольник АВС равносторонний, значит его углы равны по 60°.
2) OA = OB = 6 см, OC=8см
ΔОАС = ΔОВС по двум катетам. По теореме Пифагора в ΔОАС:
АС = √(ОА² + ОС²) = √(36 + 64) = √100 = 10 см
ВС = АС = 10 см
ΔОАВ равнобедренный прямоугольный. По теореме Пифагора
АВ = √(ОА² + ОВ²) = √(36 + 36) = 6√2 см
ΔАВС равнобедренный. По теореме косинусов найдем угол АСВ:
cosACB = (CA² + CB² - AB²)/(2·CA·CB) = (100 + 100 - 72)/(2·10·10) =
= 128/200 = 0,64
∠ACB ≈ 50°
∠CAB = ∠CBA ≈ (180° - 50°)/2 ≈ 65°
Найти биссектрису треугольника, проведенную из вершины этого угла.
----------
Пусть дан треугольник АВС. в котором сторона АС=АВ:2, а угол между этими сторонами равен 60º.
Треугольник, в котором одна сторона равна половине другой, а угол между ними равен 60º - прямоугольный.
Биссектриса АD делит угол ВАС на два угла по 30º.
Треугольник АСD прямоугольный, угол САD=30°, следовательно, угол СDА=60°
АС=3, АD=АС:cos 30°
АD=3:[(√3):2]АD=2√3
--------------------
2) В треугольнике ABC сторона AB равна 21, биссектриса BD равна 8√7 ,а отрезок DC равен 8. Найти периметр треугольника ABC.
В решении используем два свойства биссектрисы угла треугольника.
а) Квадрат биссектрисы угла треугольника равен произведению сторон, образующих угол минус произведение отрезков, на которые она делит сторону, противолежащую этому углу.⇒
L²=a*b- e*d ( L- биссектриса, e и d - отрезки противоположной углу стороны).
ВD²=АВ*ВС-АD*DС
448=21ВС-8х
21ВС=448+8х
ВС=(448+8х):21
б) Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.⇒
АВ:ВС=АD:DС
21:[(448+8х):21]=х:8
3528=448+8х² сократим на 8 и оформим квадратное уравнение:
х²+56х-441=0
Решив уравнение, получим два корня:
х1=7
х2=-63 ( не подходит)⇒
АD=7
Подставим значение АD в отношение сторон треугольника:
21:ВС=7:8
7ВС=168
ВС=24
РΔ (АВС)=АВ+ВС+А21+24+(7+8)=60 (ед. длины)
-------
К решению даны два приложения с рисунками, хотя они очень простые и можно обойтись без них.
[email protected]