Общий вид квадратного уравнение следующее
a·x²+b·x+c=0, где a≠0.
Неполное квадратное уравнение имеет один из следующих видов:
a·x²+c=0 когда b=0; a·x²+b·x=0 когда c=0;a·x² = 0 когда b=c=0.1. a) Если неполное квадратное уравнение имеет вид a·x²+c=0 и c/a<0, то квадратное уравнение a·x²+c=0 имеет корни равные по модулю, но противоположные по знаку:
a·x²+c=0 ⇔ a·x² = -c ⇔ x² = -c/a, так как -c/a>0 ⇔ 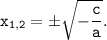
Тогда
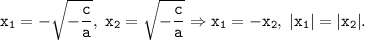
Отсюда условие:
b=0 и c/a<0!
b) Если неполное квадратное уравнение имеет вид a·x²=0, то квадратное уравнение a·x²=0 имеет единственный корень:
a·x²=0 ⇔ x²=0 ⇔ x=0.
Отсюда условие:
b=c=0!
В случае a·x²+b·x=0 квадратное уравнение имеет два корня:
a·x²+b·x=0 ⇔ x·(a·x+b)=0 ⇒ x₁=0, x₂= -b/a.
Пусть большее число равно х, тогда меньшее по условию равно х - 20. Их произведение равно y = x(x - 20) = x^2 - 20x. Для нахождения наименьшего возможного у берем производную от у и приравниваем нулю: y' = 2x - 20 = 0. Отсюда х = 10. Нетрудно проверить, что в этой точке у имеет минимум. Второе из чисел равно 10 - 20 = -10.
x и y
y=1-x
z=x(1-x)
Находим критическую точку:
z'=1-x-x=1-2x
z'=0-> x=0,5
Проверяем какой экстремум:
x<0,5->z'>0-возрастает
x>0,5->z'<0-убывает, следовательно это максимум
ответ:x= 0,5 и y= 0,5->xy=0,25