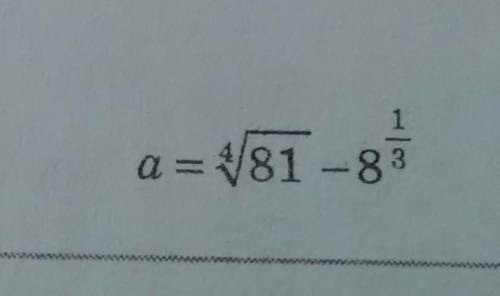
ответ: 60 деталей. 30 деталей.
Объяснение:
Решение.
Пусть второй автомат в час изготавливает х деталей. Тогда
первый автомат изготавливает х+30 деталей.
Время на изготовление 180 деталей 1 автоматом равно 180/(х+30) часов
а время для 2 автомата равно 180/х часов.
Разница во времени равна 3 часа. Составим уравнение:
180/х - 180/(х+30) = 3;
180*(x+30) - 180x = 3x(x+30);
180x+ 5400 - 180x = 3x²+90x;
3x²+90x-5400=0; [: 3]
x²+30x-1800 = 0;
x1=30; x2= -60 - не соответствует условию
х=30 деталей изготавливает 2 автомат;
х+30 = 60 деталей изготавливает 1 автомат;
(х +6 -х²)/(х +1)² ≤ 0 ( знаменатель всегда ≥ 0, причём х ≠ -1), значит числитель ≤ 0
х +6 -х² ≤ 0 ( корни 3 и -2)
-∞ -2 -1 3 +∞
- + + - это знаки х +6 -х²
ответ: х∈ (-∞; -2]∪[3; +∞)
4) (3х - х²) (х² + 2х - 8) > 0
метод интервалов.
ищем нули числителя и знаменателя:
3х - х² = 0 х² +2х - 8 = 0
корни 0 и 3 корни -4 и 2
-∞ -4 0 2 3 +∞
- - + + - это знаки 3х - х²
+ - - + + это знаки х² +2х - 8
это решение неравенства