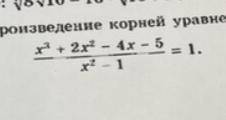
Центральный угол правильного многоугольника - это угол между двумя лучами, проведенными из центра многоугольника к двум его соседним вершинам. Центр правильного многоугольника совпадает с центром описанной окружности, значит, центральный угол, образованный двумя радиусами, проведенными к двум соседним вершинам, равен центральному углу многоугольника.
У правильного n-угольника n равных сторон, значит, будет n равных центральных углов.
Для двенадцатиугольника
360° : 12 = 30°
Внешний угол правильного многоугольника равен центральному углу.

Объяснение:
[(x³+2x²-4x-5)/(x²-1)]-1=0
(x³+2x²-4x-5-x²+1)/(x²-1)=0
x³+2x²-4x-5-x²+1=0 ; x²-1≠0
x³+x²-4x-4=0 ; x≈±1
x²(x+1)-4(x+1)=0 ; x≈±1
(x+1)(x²-4)=0 ; x≠±1
x=-1 этот корень не подходит так как x≠±1
x²=4
x=±2
x₁=-2 ; x₂=2
x₁*x₂=-2*2=-4
x₁*x₂=-4