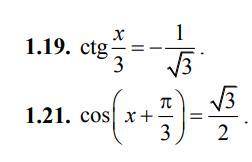
Объяснение:
1) проверим для n=3
2³=8 ; 2*3+1=7 ; 2³>2*3+1 верно (1)
2) предположим что неравенство верно при n=k (k>3) (2)
3) при n=k+1 проверим выполнение неравенства
2^(k+1)=2*2^k
2(k+1)+1=2k+3
по предположению (2) 2^k>2k+1
умножим обе части на 2
2*2^k>2(2k+1)=4k+2
2*2^k>4k+2
сравним 4k+2 и 2k+3 для этого определим знак их разности
4k+2 - (2k+3)=4k+2-2k-3=2k-3 так как k>3 то 2k>2*3=6
2k>6 и тем более 2k>3 ⇒ 2k-3>0 ⇒ 4k+2 - (2k+3)>0 ⇒ 4k+2 > (2k+3)
так как 2^(k+1)>4+2k и 4+2k>2k+3 и 2k+3=2(k+1)+1
то 2^(k+1)> 2(k+1)+1 то есть неравенство выполняется для n=k+1 (3)
из (1); (2); (3) ⇒ неравенство верно для любого n>3
ответ: 1.19 . x = 2π + 3πn , nЄ Z ; 1.21 . x = ( - π/3 ± π/6 ) + 2πn , nЄ Z .
Объяснение:
1.19 . ctgx/3 = - 1/√ 3 ;
x/3 = arcctg( - 1/√ 3) + πn , nЄ Z ;
x/3 = π - arcctg( 1/√ 3) + πn ;
x/3 = π - π/3 + πn ;
x/3 = 2π/3 + πn ; │X 3
x = 2π + 3πn , nЄ Z ;
1.21 . cos( x + π/3 ) = √ 3/2 ;
x + π/3 = ± arccos( √ 3/2) + 2πn , nЄ Z ;
x + π/3 = ± π/6 + 2πn ;
x = ( - π/3 ± π/6 ) + 2πn , nЄ Z .