a=4
(2;1)
Объяснение:
Из условия известно, что первое уравнение этой системы обращается в верное равенство при x= 8 и y= −7; тогда, подставив эти значения переменных в первое уравнение, можно найти коэффициент a.
Получим:
ax+3y=11;8a+3⋅(−7)=11;8a=11−(−21);8a=32;a=4.
При таком значении коэффициента a данная система примет вид:
{4x+3y=115x+2y=12
Для решения этой системы уравнений графически построим в одной координатной плоскости графики каждого из уравнений.
Графиком уравнения 4x+3y=11 является прямая.
Найдём две пары значений переменных x и y, удовлетворяющих этому уравнению.
x −1 2
y 5 1
Построим на координатной плоскости xОy прямую m, проходящую через эти две точки.
Графиком уравнения 5x+2y=12 также является прямая.
Найдём две пары значений переменных x и y, удовлетворяющих этому уравнению.
x 0 2
y 6 1
Построим на координатной плоскости xОy прямую n, проходящую через эти две точки.
Получим:
Прямые m и n пересекаются в точке A, координаты которой являются решением системы, т. е. A(2;1)
Объяснение:
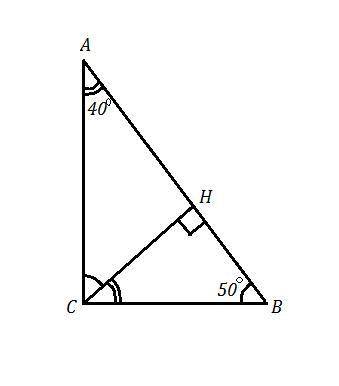
ΔАВС , ∠С=90° , ∠В=50° ⇒ ∠А=90°-∠В=90°-50°=40°
СН ⊥ АВ ⇒ ∠СНА=90° и ∠СРВ=90° .
Рассм. ΔВСН . Он прямоугольный и ∠В=50° , тогда ∠ВСН=90°-50°=40°. Это угол, образованный высотой СН с меньшим катетом (катет ВС лежит против меньшего острого угла ΔАВС).
Рассм. ΔАСН . Он прямоугольный и ∠А=40° , тогда ∠АСН=90°-40°=50°. Это угол, образованный высотой СН с бОльшим катетом АС (катет АС лежит против бОльшего острого угла ΔАВС).
Замечание. Так как у треугольников ΔАВС , ΔВСН и ΔАСН все три угла равны, то эти треугольники подобны .
Відповідь:
−4≤z≤6
Пояснення:
(z−6)(z+4)≤0.
Методом интервалов
___+-4-6+
zє[-4; 6] или −4≤z≤6