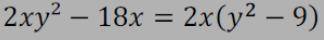
В решении.
Объяснение:
Побудуйте графік функції у = 3(х – 2)2 за до геометричних перетворень. Підготуйте таблицю значень початкової функції у = х2, вибравши зручні для побудови значення аргументу.
Постройте график функции у = 3(х – 2)² с геометрических преобразований. Подготовьте таблицу значений начальной функции
у = х², выбрав удобные для построения значения аргумента.
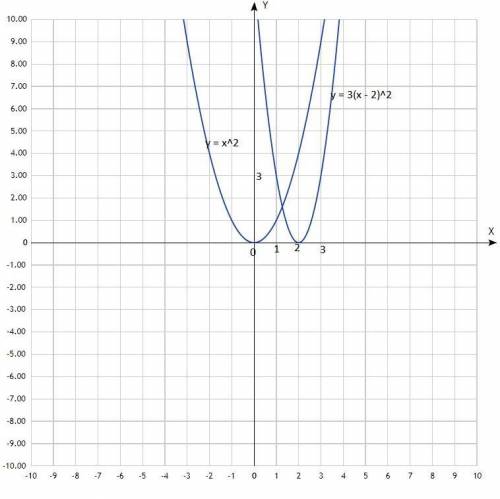
График функции у = 3(х – 2)² парабола, получен при сдвиге классической параболы у = х² на две единицы вправо и "уже" её за счёт множителя 3.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х 0 1 2 3 4
у 12 3 0 3 12
По вычисленным точкам построить параболу.
Таблица значений начальной функции у = х²:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 4 9
В решении.
Объяснение:
5) Упростить:
a) (а² - 4)/9b : (a - 2)/18b² =
= ((a - 2)(a + 2))/9b : (a - 2)/18b² =
= ((a - 2)(a + 2)*18b²)/(9b*(a - 2)) =
сократить (разделить) 9b и 18b² на 9b; (a - 2) и (a - 2) на (a - 2);
= b(a + 2);
b) (m² - n²)/14a : (m - n)/56a² =
= ((m - n)(m + n))/14a : (m - n)/56a² =
= ((m - n)(m + n)*56a²)/(14a*(m - n)) =
сократить (разделить) 56a² и 14a на 14а; (m - n) и (m - n) на (m - n);
= 4а(m + n).
6) Решить уравнение:
а) (х + 7)/(х - 2) = 10
х + 7 = 10(х - 2)
х + 7 = 10х - 20
х - 10х = -20 - 7
-9х = -27
х = -27/-9
х = 3.
b) (х - 8)/(х + 1) = -2
х - 8 = -2(х + 1)
х - 8 = -2х - 2
х + 2х = -2 + 8
3х = 6
х = 2.
2ху²-18х=2х(у²-9)
2ху²-18х=2ху²-18х
(не знаю как подробно это расписать, так как все действия в уме делаются)