y = x³ - 4x²
Найдём производную :
y' = (x³)' - 4(x²)' = 3x² - 8x
Найдём критические точки, для этого приравняем производную к нулю.
y' = 0
3x² - 8x = 0
x(3x - 8) = 0
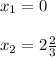
Отметим критические точки на числовой прямой и выясним знаки производной на промежутках, на которые эти точки разбивают числовую прямую .
y'(x) + - +
____________0___________2 2/3_____________
y(x) ↑ ↓ ↑
На промежутках (- ∞ ; 0] и [2 2/3 ; + ∞) -функция возрастает
На промежутке [0 ; 2 2/3] - функция уюывает
1.1.1: 504 варианта
1.1.2: 792 варианта
Объяснение:
1.1.1. Поскольку все 3 выборных должности различны, то при выборе 3 из 9 кандидатов также важен и порядок выбора. То есть требуется найти число размещений 3 элементов (выборные должности) из 9 (число кандидатов).
Это производится по формуле:
В нашем случае n=9; k=3. Т.е.
ответ: 504 различных случая возможно.
1.1.2
Поскольку у нас нет известных различий среди 5 командированных сотрудников, то порядок их выбора значения не имеет (размещение элементов внутри выборки не учитывается - считается как 1 вариант), то при выборе 5 человек из 12 кандидатов порядок выбора не важен. То есть требуется найти число сочетаний 5 элементов (число командировок) из 12 (число кандидатов).
Это производится по формуле:
В нашем случае n=15; k=5. Т.е. число сочетаний равно
792 варианта групп