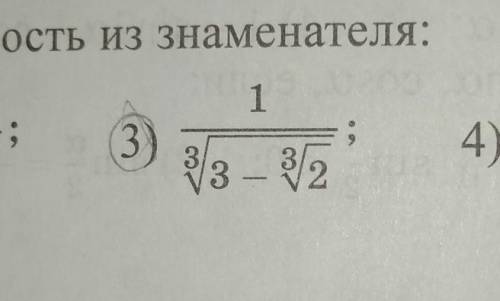
![\dfrac{1}{\sqrt[3]{3-\sqrt[3]{2}}}=\dfrac{\sqrt[3]{9+3\sqrt[3]2+\sqrt[3]4}}{\sqrt[3]{(3-\sqrt[3]2)(9+3\sqrt[3]2+\sqrt[3]4)}}=\dfrac{\sqrt[3]{9+3\sqrt[3]2+\sqrt[3]4}}{\sqrt[3]{3^3-\sqrt[3]{2^3}}}=\dfrac{\sqrt[3]{9+3\sqrt[3]2+\sqrt[3]4}}{\sqrt[3]{27-2}}=\\\\\\=\dfrac{\sqrt[3]{9+3\sqrt[3]2+\sqrt[3]4}}{\sqrt[3]{25}}=\dfrac{\sqrt[3]{9+3\sqrt[3]2+\sqrt[3]4}\cdot \sqrt[3]5}{\sqrt[3]{25}\cdot \sqrt[3]5}=\dfrac{\sqrt[3]{(9+3\sqrt[3]2+\sqrt[3]4)\cdot 5}}{\sqrt[3]{125}}=](/tpl/images/1870/1902/186f0.png)
![=\dfrac{\sqrt[3]{45+15\sqrt[3]2+5\sqrt[3]{4}}}{5}](/tpl/images/1870/1902/77ee6.png)
Пусть f(x)=ax^2+bx+c. Данные уравнения могут быть записаны в виде
ax^2+(b-5)x+(c+20)=0;\ ax^2+(b-2)x+(c+8)=0.
По условию эти уравнения имеют единственные корни, что бывает тогда и только тогда, когда их дискриминанты равны нулю, то есть
(b-5)^2-4ac-80a=0;\ (b-2)^2-4ac-32a=0.
Домножим первое выражение на 2, а второе на 5, после чего возьмем их разность:
2(b-5)^2-8ac-5(b-2)^2+20ac=0;\ 12ac=3b^2-30;\ 4ac=b^2-10,
откуда дискриминант исходного квадратного трехчлена равен
b^2-4ac=b^2-b^2+10=10.
Таким образом, дискриминант равен 10, а значит наибольшее значение, которое он может принимать, также равен 10
Есть два решения этой задачи - стандартное и на сообразительность.
Начну со второго. Учитывая, что расстояние между домами равно сумме высот дома и фонаря, нужного результата мы добьемся, если рассыпем зёрна на расстоянии 6 метров от дома. Тогда катеты левого прямоугольного треугольника равны 8 и 6 метров, правого - 6 и 14-6=8 метров. То есть эти треугольники равны, а тогда у них равны гипотенузы, чего и нужно было добиться.
Первый Если расстояние от первого дома равно x, то квадрат гипотенузы левого треугольника равен 8²+x², а квадрат гипотенузы правого треугольника равен 6²+(14-x)²; а поскольку гипотенузы по условию должны быть равны, получаем уравнение
64+x²=36+196-28x+x²; 28x=168; x=6
ответ: 6 метров